This is the course website for a previous iteration of the course. If you’re looking for the most recent course website, look at practicaldsc.org.

LARDS: Linear Algebra Review for Data Science

Designed for EECS 398-003, Fall 2024 at the University of Michigan

jump to the table of contents • last updated Saturday, August 3rd

Linear algebra is a formal prerequisite of this course. However, many students either (1) expressed interest in taking the course but didn’t satisfy the prerequisite, and hence were granted a waiver, or (2) have some linear algebra experience but would like a refresher before the course. The goal of the videos and questions below is to get you up to speed on the linear algebra you’ll need to know later on in this course. We call this page LARDS, short for Linear Algebra Review for Data Science.

Most of the videos are taken from DSC 40A, a class Suraj taught in his final quarter at UCSD. (The videos often refer to a class called Math 18, which is a linear algebra class at UCSD, similar to Math 214/217 here at Michigan.) LARDS is not a replacement for a formal linear algebra course – there are lots of ideas that are important in linear algebra that aren’t touched on here at all – but it’ll develop the skills necessary to succeed in Practical Data Science. The content here also doesn’t cover everything in linear algebra that is useful for data science; for instance, we don’t discuss eigenvalues and eigenvectors here at all, so if that material appears in Practical Data Science, we’ll cover it from the ground up.

To really learn the material here, you need to work through the provided Practice Questions! These questions are all carefully chosen to develop particular skills, and build upon each other. They’ll gauge not only how well you understood the concepts from the videos, but also build your ability to problem-solve and extrapolate from what’s given.

We know you’re still on summer break, so we’re not requiring that you submit your answers anywhere. But, it’s a good idea to work through as much as you can, regardless of your linear algebra background.

We won’t be providing answers to the Practice Questions right off the bat. Instead, we want you to attempt them on your own. If you have questions about any of the videos or problems, you can ask us on Ed, the course forum we’ll be using this fall (instead of Piazza).

🙋 Join Ed here (using your @umich.edu email)

Our hope is that these resources are useful not only to the students in this class, but also to students in other machine learning classes that have linear algebra as a prerequisite. (When we taught similar classes at UCSD and Berkeley, students struggled with applying concepts from traditional linear algebra courses to machine learning.)

LARDS is brand-new and is a work in progress. Explanations may be updated, and questions may be added/removed. If you notice any errors or typos (or have questions about LARDS but aren’t taking Practical Data Science this fall), let Suraj know at rampure@umich.edu.

Content

  1. Vectors and the dot product
  2. The dot product, angles, and orthogonality
  3. Adding and scaling vectors
  4. Linear combinations and span
  5. Linear independence
  6. Projecting onto a single vector
  7. Projecting onto the span of multiple vectors
  8. Matrices and matrix-vector multiplication
  9. Projecting onto the span of multiple vectors, again
  10. Gradients
  11. Other Resources
    1. Khan Academy
    2. 3Blue1Brown
    3. Mathematics for Machine Learning
    4. Linear Algebra for Data Science

Vectors and the dot product

📝 slides   🎥 video on YouTube

Practice Questions 1.1-1.3

Question 1.1

Consider the vectors \(\vec{u}\) and \(\vec{v}\) defined below:

\[\vec{u} = \begin{bmatrix} 1 \\ -3 \\ 8 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 3 \\ 0 \\ -1 \end{bmatrix}\]

Determine the values of the following quantities.

(a) \(\lVert \vec u \rVert\)

(b) \(\vec u \cdot \vec v\)

(c) \(\vec v^T \vec u\)

Question 1.2

Suppose that on your way home from discussion section on North Campus, you drive 2 miles east and 7 miles north. (For the purposes of this question, assume that North Campus can be represented by just a single point.)

(a) How far do you live from North Campus, in miles?

(b) Suppose we draw a horizontal line passing through North Campus, and a line passing through North Campus and your home. Determine the angle between the two lines in degrees. (You’ll need to use a calculator – Google works just fine!)

Question 1.3

Suppose \(\vec{1} \in \mathbb{R}^n\) is a vector containing the value 1 for each element, i.e. \(\vec{1} = \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix}\). For any other vector \(\vec{b} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix}\), what is the value of \(\vec{1} \cdot \vec{b}\)?

The dot product, angles, and orthogonality

📝 slides   🎥 video on YouTube

Practice Questions 2.1-2.3

Question 2.1

Consider the vectors \(\vec{u}\) and \(\vec{v}\) defined below:

\[\vec{u} = \begin{bmatrix} 1 \\ -3 \\ 8 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 3 \\ 0 \\ -1 \end{bmatrix}\]

Determine the angle between \(\vec u\) and \(\vec v\) in the form of \(\cos^{-1} ( \cdot )\). Hint: You’ll know you did this correctly if you find that, when converted to degrees, the angle between \(\vec u\) and \(\vec v\) is approximately \(101º\).

Question 2.2

Note: In addition to reviewing the concepts in the video, this question is also designed to refresh your understanding of limits from Calculus 1.

Consider the vectors \(\vec{x}\) and \(\vec{y}_c\) defined below:

\[\vec{x} = \begin{bmatrix} -4 \\ 3 \end{bmatrix} \qquad \vec{y}_c = \begin{bmatrix} 3 \\ c \end{bmatrix}\]

Here, \(c\) is an unknown real number. For example:

\[\vec{y}_2 = \begin{bmatrix} 3 \\ 2 \end{bmatrix}\]

(a) On a piece of paper (or on a tablet), draw \(\vec x\), \(\vec y_0\), \(\vec y_{20}\), and \(\vec y_{-30}\).

(b) Define \(\theta_c\) to be the angle between \(\vec{x}\) and \(\vec{y}_c\). Using properties of limits, show that:

\[\lim_{c \rightarrow \infty} \theta_c = \cos^{-1} \left( \frac{3}{5} \right)\]

(c) Is \(\cos^{-1} \left( \frac{3}{5} \right)\) the largest possible value of \(\theta_c\), or the smallest possible value?

  • If you believe this is the largest possible value of \(\theta_c\), determine the smallest possible value of \(\theta_c\).
  • If you believe this is the smallest possible value of \(\theta_c\), determine the largest possible value of \(\theta_c\).

(d) \(\cos^{-1} \left( \frac{3}{5} \right)\) – which, recall, is \(\displaystyle \lim_{c \rightarrow \infty} \theta_c\) – is also equal to the angle between \(\vec{x}\) and a particular unit vector, \(\vec u\). (A unit vector \(\vec u\) is a vector such that \(\lVert \vec u \rVert\) = 1.) What is the vector \(\vec u\)?

Question 2.3

As we saw in the first two videos, the dot product \(\vec u \cdot \vec v\) of two vectors \(\vec u, \vec v \in \mathbb{R}^n\):

  • returns a scalar – that is, a single number.
  • is valid for any \(n \geq 1\), as long as both \(\vec u\) and \(\vec v\) have the same number of components.
  • measures how similar \(\vec u\) and \(\vec v\) are.

The cross product \(\vec u \times \vec v\) of two vectors is only defined when both vectors are in \(\mathbb{R}^3\). If \(\vec{u} = \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix}\), then:

\[\vec u \times \vec v = \begin{bmatrix} u_2 v_3 - u_3 v_2 \\ u_3 v_1 - u_1 v_3 \\ u_1 v_2 - u_2 v_1 \end{bmatrix}\]

Note that the cross product of two vectors in \(\mathbb{R}^3\) is another vector in \(\mathbb{R}^3\), rather than a scalar! In particular, the cross product \(\vec u \times \vec v\) is defined to be a vector orthogonal to both \(\vec u\) and \(\vec v\), with a length of \(\lVert \vec u \rVert \lVert \vec v \rVert \sin \theta\), pointing in the direction determined by the right hand rule:

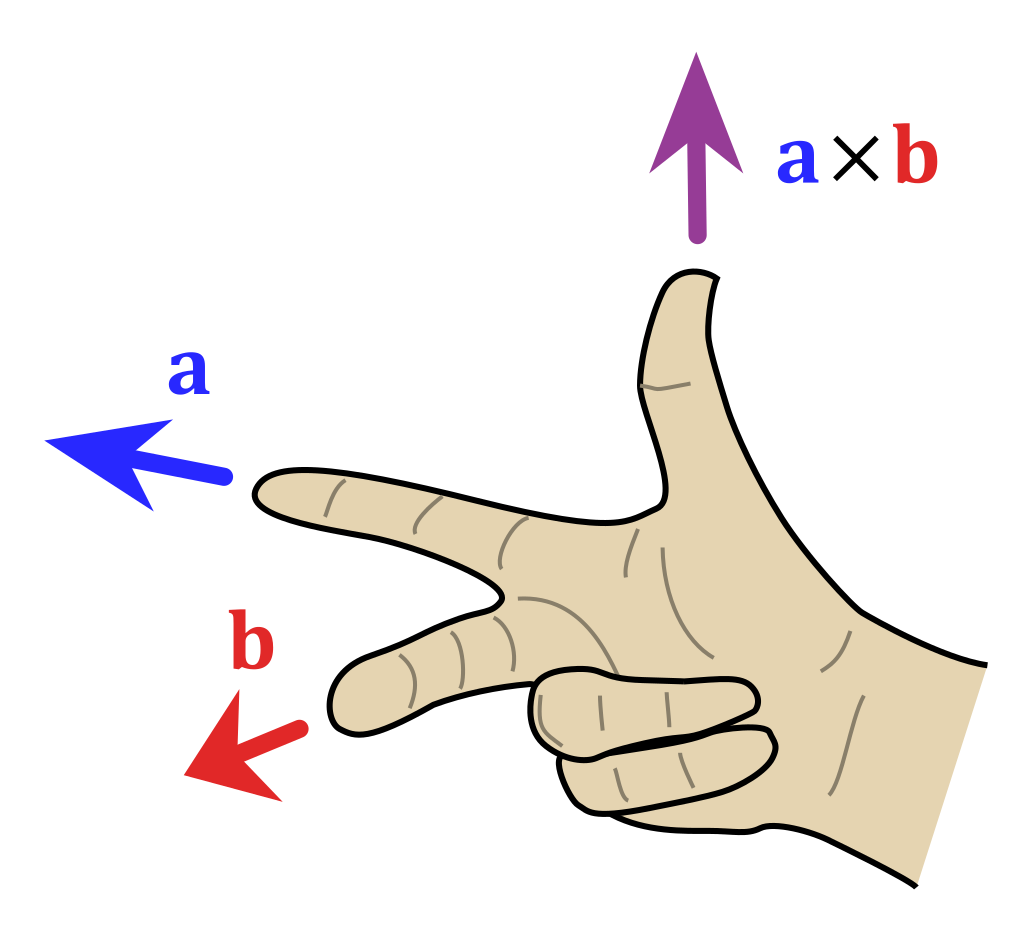
(a) Prove that \(\vec u \times \vec v\) is orthogonal to both \(\vec u\) and \(\vec v\).

(b) What is the vector \(\vec u \times \vec u\)?

(c) Once again, consider the vectors \(\vec{u}\) and \(\vec{v}\) defined below:

\[\vec{u} = \begin{bmatrix} 1 \\ -3 \\ 8 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 3 \\ 0 \\ -1 \end{bmatrix}\]

There are infinitely many vectors that are orthogonal to both \(\vec u\) and \(\vec v\), but they all point in the same direction. Determine the vector \(\vec w = \begin{bmatrix} w_1 \\ w_2 \\ w_3 \end{bmatrix}\) that is orthogonal to both \(\vec u\) and \(\vec v\) such that \(w_1 + w_2 + w_3 = 1\).

Adding and scaling vectors

📝 slides   🎥 video on YouTube

Practice Question 3.1

Question 3.1

Consider the vectors \(\vec{u}\) and \(\vec{v}\) defined below:

\[\vec{u} = \begin{bmatrix} 2 \\ -1 \\ 0 \\ 5 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 1 \\ 2 \\ 4 \\ -3 \end{bmatrix}\]

(a) Show that \(\vec u + \vec v\) and \(\vec u - \vec v\) are orthogonal.

(b) Now, suppose that \(\vec u, \vec v \in \mathbb{R}^n\) are two arbitrary vectors with the same number of components. Is it always true that \(\vec u + \vec v\) and \(\vec u - \vec v\) are orthogonal?

  • If so, prove why.
  • If not, specify conditions under which it’s guaranteed that \(\vec u + \vec v\) and \(\vec u - \vec v\) are orthogonal, and show your work.

Hint: You’ll need to use the distributive property of the dot product.

Linear combinations and span

📝 slides   🎥 video 1 (3Blue1Brown) on YouTube   🎥 video 2 on YouTube

Practice Question 4.1

Question 4.1

Consider the vectors \(\vec{a}\) and \(\vec{b}_k\) defined below:

\[\vec a = \begin{bmatrix} 2 \\ -1 \end{bmatrix} \qquad \vec{b}_k = \begin{bmatrix} k \\ 3 \end{bmatrix}\]

(a) Write \(\vec{c} = \begin{bmatrix} 2 \\ -17 \end{bmatrix}\) as a linear combination of \(\vec a\) and \(\vec{b}_2\).

(b) There is exactly one value of \(k\) such that \(\text{span}(\vec{a}, \vec{b}_k) \neq \mathbb{R}^2\). What is that value of \(k\), and why?

Linear independence

There’s no past lecture video that addresses this idea in detail, but it’s an important one.

In the 3Blue1Brown video in the section above, you saw a graphical depiction of when three vectors in \(\mathbb{R}^3\) do span all of \(\mathbb{R}^3\), and of when they don’t span all of \(\mathbb{R}^3\). But, given three vectors in \(\mathbb{R}^3\) in component form, how do we determine whether or not they span all of \(\mathbb{R}^3\)?

It turns out that this question will be of great importance to us when we study machine learning later on in the quarter. Our ability to make predictions about the future in some cases, strangely enough, will depend on whether or not a collection of \(d\) vectors in \(\mathbb{R}^n\) are linearly independent. When we get to that point, our vectors will contain data about the individuals in our dataset – for instance, we may have a height vector, that contains the height of every person in our dataset in inches, and a weight vector, that contains the weight of every person in our dataset in pounds. (That’s not terribly important right now – but it’s important to keep that in perspective. There’s a reason you need to know all of this.)

Vectors \(\vec v_1, \vec v_2, ..., \vec v_d\) are linearly independent if and only if the only solution to:

\[a_1 \vec v_1 + a_2 \vec v_2 + ... + a_d \vec v_d = \vec{0}\]

is:

\[a_1 = a_2 = ... = a_d = 0\]

If there is any solution \(a_1 \vec v_1 + a_2 \vec v_2 + ... + a_d \vec v_d = \vec{0}\) in which at least one of \(a_1, a_2, ..., a_d \neq 0\), then \(\vec v_1, \vec v_2, ... \vec v_d\) are linearly dependent.

In general, there is a computational strategy for determining whether \(d\) vectors in \(\mathbb{R}^n\) are linearly independent, which you can learn more about here. But for us, the conceptual understanding will be more useful. Intuitively, a set of vectors is linearly dependent – that is, not linearly independent – if at least one vector in the set can be written as a linear combination of other vectors in the set.

For instance, consider the vectors \(\vec{u}\), \(\vec{v}\), and \(\vec{w}\), defined below:

\[\vec{u} = \begin{bmatrix} 1 \\ -3 \\ 8 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 3 \\ 0 \\ -1 \end{bmatrix} \qquad \vec{w} = \begin{bmatrix} -1 \\ -6 \\ 17 \end{bmatrix}\]

Here, \(\vec{w} = 2 \vec{u} - \vec{v}\), which means that \(\vec{w} \in \text{span}(\vec{u}, \vec{v})\), i.e. that \(\vec{w}\) can be written as a linear combination of other vectors in the set. Therefore, vectors \(\vec{u}, \vec{v}, \vec{w}\) are not linearly independent, and are instead linearly dependent.

If you want to see how this ties into the formal definition of linear independence, note that starting with \(\vec{w} = 2 \vec{u} - \vec{v}\), we can re-arrange to get \(2 \vec{u} - \vec{v} - \vec{w} = \vec{0}\), which means that we’ve found a solution to \(a \vec{u} + b \vec{v} + c \vec{w} = \vec{0}\) that isn’t \(a = b = c = 0\). Specifically, we’ve found that \(a = 2, b = -1, c = -1\) also satisfies \(a \vec u + b \vec v + c \vec w = \vec 0\). This means, again, that \(\vec u, \vec v, \vec w\) are not linearly independent.

Practically, this means that \(\text{span}(\vec{u}, \vec{v}, \vec{w}) = \text{span}(\vec{u}, \vec{v})\), i.e. \(\vec{w}\) doesn’t “contribute” or “unlock any new vectors” to the span of just \(\vec{u}\) and \(\vec{v}\).

Thinking back to the heights and weights example, suppose that in addition to a vector that has everyone’s height in inches and another vector that has everyone’s weight in pounds, we also have a vector that has everyone’s height in centimeters. Since 1 inch = 2.54 centimeters, we’d have that:

\[\text{vector with heights in centimeters} = 2.54 (\text{vector with heights in inches})\]

which means that the vector with everyone’s height in centimeters is redundant with the vector with everyone’s height in inches. It doesn’t change the span of our vectors, and down the road, that’ll mean that it doesn’t improve the quality of our predictions.

Practice Question 5.1

Question 5.1

The scalar triple product of three vectors \(\vec u, \vec v, \vec w \in \mathbb{R}^3\) is defined as:

\[\vec u \cdot (\vec v \times \vec w)\]

The scalar triple product has several interesting properties, which you can read about here. One of the many uses of the scalar triple product is that it can be used to determine whether the vectors \(\vec u, \vec v, \vec w\) are linearly independent! Specifically, if the scalar triple product is equal to 0, then \(\vec u, \vec v, \vec w\) are linearly dependent; otherwise, \(\vec u, \vec v, \vec w\) are linearly independent.

(Remember that the cross product is only defined for two vectors in \(\mathbb{R}^3\), meaning that the scalar triple product is only defined for three vectors in \(\mathbb{R}^3\). In all other cases, we’d need to use some other technique for determining whether the vectors are linearly independent.)

(a) Using the scalar triple product, determine whether or not the three vectors defined below are linearly independent.

\[\vec{u} = \begin{bmatrix} 1 \\ -3 \\ 8 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 3 \\ 0 \\ -1 \end{bmatrix} \qquad \vec{w} = \begin{bmatrix} 3 \\ 2 \\ -2 \end{bmatrix}\]

(b) Suppose again that \(\vec u, \vec v, \vec w \in \mathbb{R}^3\) are arbitrary vectors. Argue why it must be the case that, if the scalar triple product \(\vec u \cdot (\vec v \times \vec w)\) is equal to 0, then \(\vec u\) must be in \(\text{span}(\vec{v}, \vec{w})\), indicating that \(\vec u, \vec v, \vec w\) are not linearly independent.

Projecting onto a single vector

📝 slides   🎥 video on YouTube

Practice Questions 6.1-6.2

Question 6.1

Before we get into any calculations, we’ll start by recapping the most recent video through some proofs. Our conclusion was that the vector in \(\text{span}(\vec x)\) that was closest to \(\vec y\) was the vector \(w^* \vec x\), where:

\[w^* = \frac{\vec x \cdot \vec y}{\vec x \cdot \vec x}\]

(a) Use the dot product to show that \(\vec y - w^* \vec x\) is orthogonal to \(\vec x\).

(b) Consider the function \(\text{error}(w) = \lVert \vec y - w \vec x \rVert\). Note that \(\text{error}\) takes in a single real number as input and returns a single real number as output.

Show, using calculus, that \(w^*\) minimizes \(\text{error}(w)\). Hint: Note that minimizing \(\lVert \vec y - w \vec x \rVert\) is equivalent to minimizing \(\lVert \vec y - w \vec x \rVert^2\), and that if \(\vec v\) is a vector, then \(\lVert \vec v \rVert^2 = \vec v \cdot \vec v\).

Question 6.2

Vectors get lonely, and so we will give each vector one friend to keep them company.

Specifically, if \(\vec{v} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix}\), \(\vec{v}_f\) is the friend of \(\vec v\), where \(\vec{v}_f = \begin{bmatrix} -v_2 \\ v_1 \end{bmatrix}\).

(a) Prove that \(\vec{v}\) and \(\vec{v}_f\) are orthogonal.

Now, consider the vectors \(\vec{c}\) and \(\vec{d}\) defined below:

\[\vec{c} = \begin{bmatrix} 1 \\ 7 \end{bmatrix} \qquad \vec{d} = \begin{bmatrix} -2 \\ 1 \end{bmatrix}\]

The next few parts ask you to write various vectors as scalar multiples of either \(\vec c\), \(\vec{c}_f\), \(\vec{d}\), or \(\vec{d}_f\), where \(\vec{c}_f\) and \(\vec{d}_f\) are the friends of \(\vec{c}\) and \(\vec{d}\), respectively. In each part, you should select one of the four vectors provided, and fill a scalar in the blank. Part of part (b) is done for you.

(b) A vector in \(\text{span}(\vec d)\) that is twice as long as \(\vec d\).

\[\underset{\text{scalar goes here}}{\underline{\hspace{0.5in}}} \qquad \times \qquad \qquad \underbrace{\vec{c} \qquad \qquad \vec{c}_f \qquad \qquad \boxed{\vec{d}} \qquad \qquad \vec{d}_f}_{\text{pick one of these four}}\]

(c) The projection of \(\vec c\) onto \(\text{span}(\vec d)\).

\[\underset{\text{scalar goes here}}{\underline{\hspace{0.5in}}} \qquad \times \qquad \qquad \underbrace{\vec{c} \qquad \qquad \vec{c}_f \qquad \qquad \vec{d} \qquad \qquad \vec{d}_f}_{\text{pick one of these four}}\]

(d) The error vector of the projection of \(\vec c\) onto \(\text{span}(\vec d)\).

\[\underset{\text{scalar goes here}}{\underline{\hspace{0.5in}}} \qquad \times \qquad \qquad \underbrace{\vec{c} \qquad \qquad \vec{c}_f \qquad \qquad \vec{d} \qquad \qquad \vec{d}_f}_{\text{pick one of these four}}\]

(e) The projection of \(\vec d\) onto \(\text{span}(\vec c)\).

\[\underset{\text{scalar goes here}}{\underline{\hspace{0.5in}}} \qquad \times \qquad \qquad \underbrace{\vec{c} \qquad \qquad \vec{c}_f \qquad \qquad \vec{d} \qquad \qquad \vec{d}_f}_{\text{pick one of these four}}\]

(f) The error vector of the projection of \(\vec d\) onto \(\text{span}(\vec c)\).

\[\underset{\text{scalar goes here}}{\underline{\hspace{0.5in}}} \qquad \times \qquad \qquad \underbrace{\vec{c} \qquad \qquad \vec{c}_f \qquad \qquad \vec{d} \qquad \qquad \vec{d}_f}_{\text{pick one of these four}}\]

Note that this question appeared in an exam for the class these videos are from!

Projecting onto the span of multiple vectors

📝 slides   🎥 video 1 on YouTube   🎥 video 2 (animation by Jack Determan) on YouTube

Matrices and matrix-vector multiplication

📝 slides   🎥 video on YouTube

Practice Questions 7.1-7.2

Question 7.1

Suppose \(M \in \mathbb{R}^{m \times n}\) is a matrix, \(\vec{v} \in \mathbb{R}^n\) is a vector, and \(s \in \mathbb{R}\) is a scalar.

Determine whether each of the following quantities is a matrix, vector, scalar, or undefined. If the result is a matrix or vector, determine its dimensions.

(a) \(M\vec{v}\)

(b) \(\vec{v} M\)

(c) \(\vec{v}^2\)

(d) \(M^TM\)

(e) \(MM^T\)

(f) \(\vec{v}^T M \vec{v}\)

(g) \((sM\vec{v}) \cdot (sM\vec{v})\)

(h) \((s \vec{v}^T M^T)^T\)

(i) \(\vec{v}^T M^T M \vec{v}\)

(j) \(\vec{v}\vec{v}^T + M^TM\)

(k) \(\frac{M \vec{v}}{\lVert \vec{v} \rVert} + (\vec{v}^T M^T M \vec{v}) M \vec{v}\)

Question 7.2

Consider the matrix \(X\) and vector \(\vec w\) defined below:

\[X = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \\ 5 & 1 & -2 \end{bmatrix} \qquad \vec{w} = \begin{bmatrix} 4 \\ 3 \\ -1 \end{bmatrix}\]

(a) Evaluate \(X \vec{w}\).

(b) As we learned in the video above, the matrix-vector product \(X \vec{w}\) is a linear combination of the columns of the matrix, \(X\), using weights from the vector \(\vec{w}\).

Fill in each blank below with a single number from the start of Question 13.

\[X \vec{w} = \underline{\hspace{0.5cm}} \begin{bmatrix} \underline{\hspace{0.5cm}} \\ \underline{\hspace{0.5cm}} \\ \underline{\hspace{0.5cm}} \end{bmatrix} + \underline{\hspace{0.5cm}} \begin{bmatrix} \underline{\hspace{0.5cm}} \\ \underline{\hspace{0.5cm}} \\ \underline{\hspace{0.5cm}} \end{bmatrix} + \underline{\hspace{0.5cm}} \begin{bmatrix} \underline{\hspace{0.5cm}} \\ \underline{\hspace{0.5cm}} \\ \underline{\hspace{0.5cm}} \end{bmatrix}\]

(c) Let’s generalize the idea from part (b). Now, suppose \(X \in \mathbb{R}^{n \times d}\) is a matrix whose columns, \(\vec{x}^{(1)}, \vec{x}^{(2)}, ..., \vec{x}^{(d)}\) are all vectors in \(\mathbb{R}^n\), and suppose that \(\vec{w} \in \mathbb{R}^d\).

Fill in the blanks:

\[X \vec{w} = \sum_{i = 1}^{\boxed{\:\:\:}} \boxed{\:\:\:}\]

(e) Evaluate \(X^TX\) and \(XX^T\).

Projecting onto the span of multiple vectors, again

Before watching the following video, you may want to review the idea of matrix inverses – here’s a link to a relevant lesson on Khan Academy.

The video below summarizes the last few videos on projections. It doesn’t introduce any new content – so you don’t need it to solve the questions below – but you may want to watch it nevertheless for review.

📝 slides 1   📝 slides 2   🎥 video 1 on YouTube   🎥 video 2 on YouTube

Practice Question 8.1

Question 8.1

Consider the vectors \(\vec{u}\), \(\vec{v}\), defined below:

\[\vec{u} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}\]

We define \(X \in \mathbb{R}^{3 \times 2}\) to be the matrix whose first column is \(\vec u\) and whose second column is \(\vec v\).

(a) In this part only, let \(\vec y = \begin{bmatrix} -1 \\ k \\ 252 \end{bmatrix}\). Find a scalar \(k\) such that \(\vec y\) is in \(\text{span}(\vec u, \vec v)\).

(b) Show that:

\[(X^TX)^{-1}X^T = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} \end{bmatrix}\]

Hint: If \(A = \begin{bmatrix} a_1 & 0 \\ 0 & a_2 \end{bmatrix}\), then \(A^{-1} = \begin{bmatrix} \frac{1}{a_1} & 0 \\ 0 & \frac{1}{a_2} \end{bmatrix}\).

(c) Now, let \(\vec y = \begin{bmatrix} 4 \\ 2 \\ 8 \end{bmatrix}\).

Find scalars \(a\) and \(b\) such that \(a \vec u + b \vec v\) is the vector in \(\text{span}(\vec u, \vec v)\) that is as close to \(\vec y\) as possible.

(d) Let \(\vec e = \vec y - (a \vec u + b \vec v)\), where \(a\) and \(b\) are the values you found in part (c).

You should notice that the sum of the entries in \(\vec e\) is 0. Why is that the case?

Gradients

The concepts explained above are typically covered – or, are related to what’s covered – in a linear algebra course. In addition to all of that, though, we’ll also need a few concepts that are traditionally covered in a multivariate calculus course, such as Math 215.

To start, let’s remember the idea of derivatives from single variable calculus. Consider, for example, the function \(f(t) = 5t^4 - t^3 - 5t^2 + 2t - 9\). Then, we have:

  • The derivative, \(\frac{df}{dt}(t) = 20t^3 - 3t^2 - 10t + 2\), is the slope of the tangent line to \(f\) at the point \((t, f(t))\). For example, at \(t = 0\), the derivative is 2, which means the slope of the tangent line at \((0, -9)\) is 2.
  • The derivative at a point describes the instantaneous rate of change of the function at that point – the larger the derivative is at a point, the more quickly the function is increasing at that point (i.e. the steeper it is).
  • The closer \(t\) is to a minimum, the shallower the slope of the tangent line is – at a minimum, the slope of the tangent line is 0!
The animation above might automatically start playing – to restart it, click "⏯️ Stop animation" and then "▶️ Start animation."

Moving forward, we will encounter functions that take in multiple inputs, such as:

\[f(x, y) = (x - 2)^2 + 2x - (y - 3)^2\]

The graph of a function like this is a surface in 3 dimensions.

Now, since \(f\) has multiple input variables, it has multiple rates of change – one in the \(x\) direction and one in the \(y\) direction. So, instead of just a single derivative, \(f\) has two partial derivatives, \(\frac{\partial f}{\partial x}\) and \(\frac{\partial f}{\partial y}\).

\(\frac{\partial f}{\partial x}\) describes the rate of change in the \(x\) direction – that is, the rate of change of \(f\) when \(x\) changes, but \(y\) is held constant. To compute \(\frac{\partial f}{\partial x}\), we treat \(y\) as a constant and take the derivative with respect to \(x\). Since \(f(x, y) = (x - 2)^2 + 2x - (y - 3)^2\), we have that:

\[\frac{\partial f}{\partial x} = 2(x-2) + 2 \qquad \frac{\partial f}{\partial y} = -2(y-3)\]

We expand on this idea, and its connection to linear algebra, below, but it’s advised that you first work through the following articles on Khan Academy:

📝 slides   🎥 video on YouTube

Practice Questions 9.1-9.2

Question 9.1

Suppose \(g: \mathbb{R}^2 \rightarrow \mathbb{R}\) is the function:

\[g(\vec x) = (x_1 - 3)^2 + (x_1^2 - x_2)^2\]

(a) Find \(\nabla g(\vec x)\), the gradient of \(g\), and use it to show that \(\nabla g \left( \begin{bmatrix} -1 \\ 1 \end{bmatrix} \right) = \begin{bmatrix} -8 \\ 0 \end{bmatrix}\).

(b) Using \(\nabla g(\vec x)\), determine the vector \(\vec x^*\) that minimizes the output of \(g\). How can you tell, without the use of any second derivative tests, that \(g\) has a global minimum?

Question 9.2

(a) Suppose \(\vec{a} \in \mathbb{R}^3\), and suppose \(f: \mathbb{R}^3 \rightarrow \mathbb{R}\) is the function:

\[f(\vec x) = \vec{a}^T \vec{x} = a_1x_1 + a_2x_2 + a_3x_3\]

What is the gradient of \(f\)?

(b) Suppose \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) is the function:

\[f(\vec x) = \vec x \cdot \vec x = x_1^2 + x_2^2 + ... + x_n^2\]

What is the gradient of \(f\)?

Other Resources

The videos below are more detailed than those above, covering lots of important ideas we didn’t touch on above (and won’t get a chance to cover in Practical Data Science).

Khan Academy

For more depth and added explanations, take a look at Khan Academy’s linear algebra course. Specifically, look at:

  1. All of Unit 1: Vectors and spaces.
  2. The first four lessons in Unit 2: Matrix transformations, through Inverse functions and transformations.
  3. The first two lessons in Unit 3: Alternate coordinate systems (bases), through Orthogonal projections. Understanding the content of the orthogonal projections lesson is the primary learning objective of LARDS.

In addition, look at Khan Academy’s Multivariable calculus course, specifically:

  1. Most of Unit 1: Thinking about multivariable functions, though the lesson on Visualizing vector-valued functions is not necessary.
  2. The first three lessons in Unit 2: Derivatives of multivariable functions, through Partial derivative and gradient. (These are also linked above.)

3Blue1Brown

Grant Sanderson (3Blue1Brown) produces excellent visual explanations of a lot of ideas that are central to data science, including neural networks, but also linear algebra. His Essence of Linear Algebra series overlaps a fair bit with the videos we’ve provided above, but with some content missing (namely, projecting onto the span of multiple vectors) and other content more heavily emphasized (e.g. the idea of a linear transformation). The series exists in two forms:

Either way, (at least) the first 9 chapters are relevant to us.

Mathematics for Machine Learning

Mathematics for Machine Learning, by Garrett Thomas, is a document that discusses the mathematics relevant for machine learning in much greater detail than we’ll need in this course. It’s quite advanced, so don’t be alarmed if the material there feels inaccessible. (More of it will make sense after Practical Data Science!)


Have other resources you think we should add here? Let us know!

Linear Algebra for Data Science

If you’d prefer to read a more formal textbook on these ideas, take a look at Linear Algebra for Data Science by Wanmo Kang and Kyunghyun Cho (a PDF is available at the linked site). Specifically, read Chapters 1-4.