♾️ Maximum Likelihood Estimation
Table of contents
Overview
In Lecture 14, we discussed the relationship between probability and statistics:
- In probability questions, we’re given some model of how the universe works, and it’s our job to determine how various samples could turn out.
Example: If we have 5 blue marbles and 3 green marbles and pick 2 at random, what are the chances we see one marble of each? - In statistics questions, we’re given information about a sample, and it’s our job to figure out how the universe – or data generating process works.
Example: Repeatedly, I picked 2 marbles at random from a bag with replacement. I don’t know what’s inside the bag. One time, I saw 2 blue marbles, then next time I saw 1 of each, the next time I saw 2 red marbles, and so on. What marbles are inside the bag?
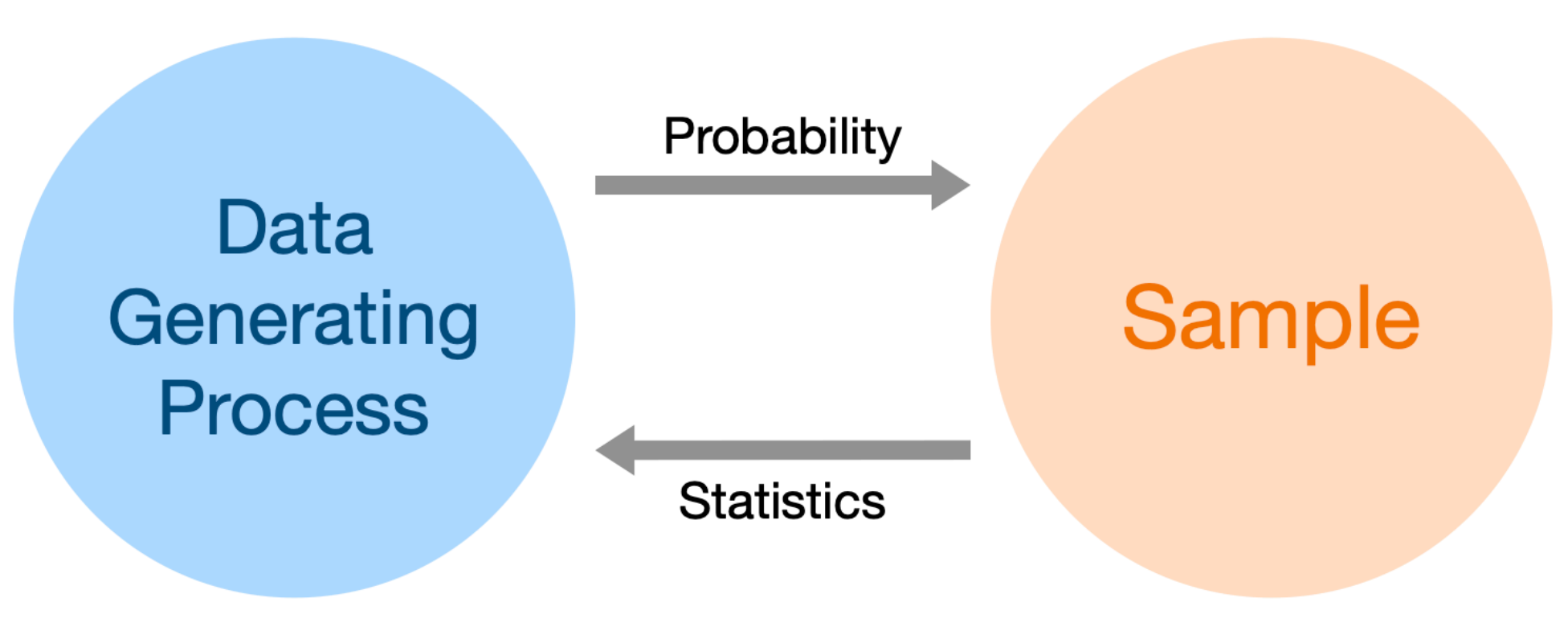
In this note, we’ll gain a deeper understanding of this relationship, through the lens of your probability knowledge from EECS 203. After reading this note, you’ll be well-equipped to tackle Question 4 on Homework 7 (and also have better context for machine learning, more generally).
Problem Setup
Let’s work with the example mentioned in Lecture 14, Slide 13. Suppose we find a coin on the ground, and we’re unsure of whether the coin is fair. We decide to flip the coin repeatedly to estimate its bias, \(\theta\), which is the probability of flipping heads on any particular flip. (The probability of flipping tails on any particular flip, then, is \(1 - \theta\)).
Suppose we flip the coin 100 times and see 65 heads. Assuming that each flip is independent, this is a possible result, no matter what the value of \(\theta\) is, as long as \(0 < \theta < 1\). But, some values of \(\theta\) are more believable than others:
- For example, if \(\theta = 0.5\), the chances of seeing 65 heads and 35 tails is:
- If \(\theta = 0.7\), the chances of seeing 65 heads and 35 tails is:
Again, the true bias, \(\theta\), could be anything, and we don’t truly know what it is, since we just found this coin on the ground. But, as we see above, some values of \(\theta\) are more likely than others – for instance, it seems that \(\theta = 0.7\) is more likely than \(\theta = 0.5\), because the probability of our observation is higher if we assume \(\theta = 0.7\) than if we assume \(\theta = 0.5\).
\(\theta = 0.5\) and \(\theta = 0.7\) were arbitrarily chosen values of \(\theta\), just for illustration. The question is, what is the most likely value of \(\theta\), among all possible \(\theta\)’s?
The Likelihood Function
To answer this question, we’ll define what’s known as the likelihood function of \(\theta\), denoted \(L(\theta)\):
\[L(\theta) = \mathbb{P}(65 \text{ heads} \: | \: \theta) = {\binom{100}{65}} \theta^{65} (1-\theta)^{35}\]We’ve used the binomial distribution, which you saw in EECS 203, to calculate the probability of seeing 65 heads and 35 tails, given a bias of \(\theta\). The function \(L(\theta)\) is given the special name of “likelihood” because it helps us measure how likely a particular value of \(\theta\) is. It emphasizes that \(\theta\) is unknown, whereas in most classical probability examples you’ve dealt with, \(\theta\) was known, but the number of heads (for example) was unknown.
\(\theta\) is referred to as a parameter of the binomial distribution, and our goal is to estimate \(\theta\) as best as we can, given our data. The word parameter here means the same as it did in Lecture 14 – a parameter defines the relationship between the inputs and outputs of a model, and we’re using the data we’re given to find optimal parameters. Here, the model is a binomial one, which takes in a number of heads and outputs the probability of seeing that many heads.
Let’s look at a plot of \(L(\theta)\) for various values of \(\theta\).
You should notice that \(L(\theta)\) peaks at 0.65, which is the empirical proportion of heads – remember that we saw 65 heads in 100 flips of this coin!
Maximizing Likelihood
Let’s see if we can prove that this is always the case – that is, let’s prove that the most likely bias of a coin, \(\theta\), when we flip it many times, is \(\frac{\text{number of heads}}{\text{total number of flips}}\).
First, let’s pose the problem more generally. If we have a coin that flips heads with probability \(\theta\), the probability of seeing \(k\) heads in \(n\) independent flips of the coin is:
\[L(\theta) = \mathbb{P}(k \text{ heads} \: | \: \theta) = {n \choose k} \theta^k (1-\theta)^{n-k}\]The question at hand is, which value of \(\theta\) maximizes \(L(\theta)\)? This resembles a question we dealt with in Lecture 14 – which value of \(h\) minimizes \(R_\text{sq}(h)\)? – the only difference being that there, we minimized, and here, we’re maximizing.
\(L(\theta)\) is a function of a single variable. To find the value of \(\theta\) that maximizes it, we can follow the same process from Lecture 14, where we take its derivative with respect to \(\theta\), and solve for the value of \(\theta\) that makes the derivative 0.
Let’s do it. To find the derivative of \(L(\theta)\) with respect to \(\theta\), we’ll need to use the power, product, and chain rules from calculus. Here we go!
\[\begin{align*} L(\theta) &= { n \choose k } \theta^k (1-\theta)^{n-k} \\ \frac{d}{d\theta}L(\theta) &= { n \choose k } \big( k\theta^{k-1} (1-\theta)^{n-k} + \theta^k (n-k)(1-\theta)^{n-k-1}(-1) \big) \end{align*}\]Now, we’ll set this to 0 and solve for the \(\theta\) that makes this happen. We’re going to call the resulting value \(\theta^*\), to emphasize that it’s the “best” \(\theta\) in some sense.
\[\begin{align*} { n \choose k }\cdot \left( k\theta^{k-1} (1-\theta)^{n-k} + \theta^k (n-k)(1-\theta)^{n-k-1}(-1) \right) &= 0 \\ k\theta^{k-1} (1-\theta)^{n-k} - \theta^k (n-k)(1-\theta)^{n-k-1} &= 0 \\ k\theta^{k-1} (1-\theta)^{n-k} &= \theta^k (n-k)(1-\theta)^{n-k-1} \\ k (1-\theta) &= \theta (n-k) \\ k - \theta k &= \theta n - \theta k \\ k &= \theta n \\ \theta^* &= \boxed{\frac{k}{n}} \end{align*}\]Since \(\theta^* = \frac{k}{n}\) is the input to \(L(\theta)\) that maximizes the likelihood function, \(L(\theta)\), we call \(\theta^*\) the maximum likelihood estimate of \(\theta\).
In our example, \(k = 65\) and \(n = 100\), which means the maximum likelihood estimate of the bias of the coin we found on the ground is \(\frac{65}{100} = 0.65\)! This matches what we saw in the graph earlier, and also shouldn’t be surprising. In our 100 flips of this random coin off the ground, we saw 65 heads and 35 tails, and so while the bias of the coin could be anything, the most likely bias of the coin is \(\theta = 0.65\).
We’ve now walked through a full example of the method of maximum likelihood estimation.
Maximizing Log Likelihood
The process of solving for \(\theta^*\) was messy, because taking the derivative of \(L(p)\) was messy, since it involved using the power, product, and chain rules!
It turns out that there’s a simplification we can use here to make our lives easier, that is often used in machine learning and statistics.
Fact: If \(x^*\) maximizes \(f(x)\), then \(x^*\) also maximizes \(\log f(x)\).
Related, if \(x^*\) minimizes \(f(x)\), then \(x^*\) also minimizes \(\log f(x)\).
To see why this is true, let’s plot a graph of \(\log L(\theta)\) vs. \(\theta\):
While the graph of \(\log L(\theta)\) looks very different than the graph of \(L(\theta)\), they are both maximized at the same position, \(\theta^* = 0.65\). The reason for this is that \(\log\) is monotonically increasing, meaning that if \(a > b\), then \(\log(a) > \log(b)\). The consequence of this is that if \(L(0.65)\) is bigger than \(L(\theta)\) for any other \(\theta\), then \(\log L(0.65)\) is bigger than \(\log L(\theta)\) for any other \(\theta\), too.
You may be wondering, and rightfully so:
Suraj, why did you randomly bring out the \(\log\) function – isn’t this explanation already long and mathematical enough?
It turns out that maximizing \(\log L(\theta)\) is way easier than maximizing \(L(\theta)\)! Here, let’s work through it. First, let’s simplify \(\log L(\theta)\). Note that we could use any base on our logarithm, but the calculations are simplest if we use the natural logarithm (which we’ll just denote with \(\log\)).
\[\begin{align*} L(\theta) &= {n \choose k} \theta^k (1-\theta)^{n-k} \\ \log L(\theta) &= \log \left( {n \choose k} \theta^k (1-\theta)^{n-k} \right) \\ &= \log {n \choose k} + \log \left(\theta^k \right) + \log \left((1 - \theta)^{n-k}\right) \\ &= \log {n \choose k} + k \log \theta + (n - k) \log (1 - \theta) \end{align*}\]Now, let’s take the derivative of \(\log L(\theta)\) and set it to 0:
\[\begin{align*} \log L(\theta) &= \log {n \choose k} + k \log \theta + (n - k) \log (1 - \theta) \\ \frac{d}{d\theta} \log L(\theta) &= 0 + k \cdot \frac{1}{\theta} + (n - k) \cdot\frac{1}{1 - \theta}(-1) = \frac{k}{\theta} - \frac{n - k}{1 - \theta} \\ 0 &= \frac{k}{\theta} - \frac{n - k}{1 - \theta} \\ \frac{k}{\theta} &= \frac{n - k}{1 - \theta} \\ k - \theta k &= \theta n - \theta k \\ k &= \theta n \\ \theta^* &= \boxed{\frac{k}{n}} \end{align*}\]By taking the log of \(L(\theta)\), we were able to find the maximum likelihood estimate, \(\theta^*\), without needing to find the derivative of \(L(\theta)\), which involved working with expressions like \(k\theta^{k-1} (1-\theta)^{n-k} + \theta^k (n-k)(1-\theta)^{n-k-1}(-1)\).
The benefit of the log function is that it turns products into sums – that is, \(\log(a \cdot b) = \log(a) + \log(b)\) – which allows us to bypass using the messy product rule.
Summary
- We found a coin on the ground, which flips heads with an unknown probability, \(\theta\).
- We flipped the coin 100 times and saw 65 heads.
To estimate the bias of the coin, we decided to use maximum likelihood estimation, which requires us to define the likelihood function for \(\theta\):
\[L(\theta) = \mathbb{P}(k \text{ heads} \: | \: \theta) = {n \choose k} \theta^k (1-\theta)^{n-k}\]in the example stated above, \(k = 65\) and \(n = 100\).
- The most likely value of \(\theta\) is the one that maximizes \(L(\theta)\).
- To make the math simpler, instead of maximizing \(L(\theta)\) directly, we maximized \(\log L(\theta)\). This found us the same maximum likelihood estimate, \(\theta^* = \frac{k}{n}\).