from lec_utils import *
import re

Lecture 12

Text as Data

EECS 398-003: Practical Data Science, Fall 2024

practicaldsc.org • github.com/practicaldsc/fa24

Announcements 📣

• Homework 5 is due tonight. It includes a required Pre-Midterm Survey.
  Homework 6 will be released later this week, but won't be due until after Fall Break.
• The Midterm Exam is on Wednesday, October 9th from 7-9PM.
  • Lectures 1-12 and Homeworks 1-6 are in scope.
  • The lecture before the exam will be review, and the TAs will run a review session on Monday from 6-8PM in FXB 1109 too.
  • You can bring one double-sided 8.5"x11" notes sheet that you handwrite yourself (no printing, no using an iPad, etc.).
  • Work through old exam problems here.
• Looking for sources of data, or other supplemental resources? Look at our updated Resources page!

Aside: Following along with lecture

• I've read the feedback, and I'll try and type slower and have slightly more of the code filled in the notebook before presenting.

• But, remember that all of the code I write live is posted before lecture – click the 📝 filled html buttons to see these (or open lecXX-filled.ipynb).

Agenda

• From text to numbers.
• Bag of words 💰.
• TF-IDF.
• Example: State of the Union addresses 🎤.

Activity

This is an old exam question!

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

From text to numbers

---

From text to numbers

• How do we represent a text document using numbers?

• Computers and mathematical formulas are designed to work with numbers, not words.

• So, if we can convert documents into numbers, we can:
  • summarize documents by finding their most important words (today).
  • quantify the similarity of two documents (today).
  • use a document as input in a regression or classification model (second half of the semester).

Example: State of the Union addresses 🎤

• Each year, the sitting US President delivers a "State of the Union" address. The 2024 State of the Union (SOTU) address was on March 7th, 2024.
  "Address" is another word for "speech."

from IPython.display import YouTubeVideo
YouTubeVideo('cplSUhU2avc')

• The file 'data/stateoftheunion1790-2024.txt' contains the transcript of every SOTU address since 1790.

with open('data/stateoftheunion1790-2024.txt') as f:
    sotu = f.read()

# The file is over 10 million characters long!
len(sotu) / 1_000_000

10.616051

Terminology

• In text analysis, each piece of text we want to analyze is called a document.
  Here, each speech is a document.

• Documents are made up of terms, i.e. words.

• A collection of documents is called a corpus.
  Here, the corpus is the set of all SOTU speeches from 1790-2024.

Extracting speeches

• In the string sotu, each document is separated by '***'.

speeches_lst = sotu.split('\n***\n')[1:]
len(speeches_lst)

234

• Note that each "speech" currently contains other information, like the name of the president and the date of the address.

print(speeches_lst[-1][:1000])

State of the Union Address
Joseph R. Biden Jr.  
March 7, 2024

Good evening. 

Mr. Speaker. Madam Vice President. Members of Congress. My Fellow Americans. 

In January 1941, President Franklin Roosevelt came to this chamber to speak to the nation. 

He said, “I address you at a moment unprecedented in the history of the Union.” 

Hitler was on the march. War was raging in Europe. 

President Roosevelt’s purpose was to wake up the Congress and alert the American people that this was no ordinary moment.   

Freedom and democracy were under assault in the world. 

Tonight I come to the same chamber to address the nation. 

Now it is we who face an unprecedented moment in the history of the Union. 

And yes, my purpose tonight is to both wake up this Congress, and alert the American people that this is no ordinary moment either. 

Not since President Lincoln and the Civil War have freedom and democracy been under assault here at home as they are today. 

What makes our moment rare is th

• Let's extract just the text of each speech and put it in a DataFrame.
  Along the way, we'll use our new knowledge of regular expressions to remove capitalization and punctuation, so we can just focus on the content itself.

def create_speeches_df(speeches_lst):
    def extract_struct(speech):
        L = speech.strip().split('\n', maxsplit=3)
        L[3] = re.sub(r"[^A-Za-z' ]", ' ', L[3]).lower() # Replaces anything OTHER than letters with ' '.
        L[3] = re.sub(r"it's", 'it is', L[3])
        return dict(zip(['president', 'date', 'text'], L[1:]))
    speeches = pd.DataFrame(list(map(extract_struct, speeches_lst)))
    speeches.index = speeches['president'].str.strip() + ': ' + speeches['date']
    speeches = speeches[['text']]
    return speeches

speeches = create_speeches_df(speeches_lst)
speeches

	text
George Washington: January 8, 1790	fellow citizens of the senate and house of re...
George Washington: December 8, 1790	fellow citizens of the senate and house of re...
George Washington: October 25, 1791	fellow citizens of the senate and house of re...
...	...
Joseph R. Biden Jr.: March 1, 2022	madam speaker madam vice president and our ...
Joseph R. Biden Jr.: February 7, 2023	mr speaker madam vice president our firs...
Joseph R. Biden Jr.: March 7, 2024	good evening mr speaker madam vice presi...

234 rows × 1 columns

Quantifying speeches

• Our goal is to produce a DataFrame that contains the most important terms in each speech, i.e. the terms that best summarize each speech:

	most important terms
George Washington: January 8, 1790	your, proper, regard, ought, object
George Washington: December 8, 1790	case, established, object, commerce, convention
...	...
Joseph R. Biden Jr.: February 7, 2023	americans, down, percent, jobs, tonight
Joseph R. Biden Jr.: March 7, 2024	jobs, down, get, americans, tonight

• To do so, we will need to come up with a way of assigning a numerical score to each term in each speech.
  We'll come up with a score for each term such that terms with higher scores are more important!

	jobs	down	commerce	...	convention	americans	tonight
George Washington: January 8, 1790	0.00e+00	0.00e+00	3.55e-04	...	0.00e+00	0.00e+00	0.00e+00
George Washington: December 8, 1790	0.00e+00	0.00e+00	1.10e-03	...	1.18e-03	0.00e+00	0.00e+00
...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: February 7, 2023	2.73e-03	1.78e-03	0.00e+00	...	0.00e+00	1.56e-03	3.34e-03
Joseph R. Biden Jr.: March 7, 2024	1.77e-03	1.96e-03	5.93e-05	...	0.00e+00	2.37e-03	3.90e-03

• In doing so, we will represent each speech as a vector.

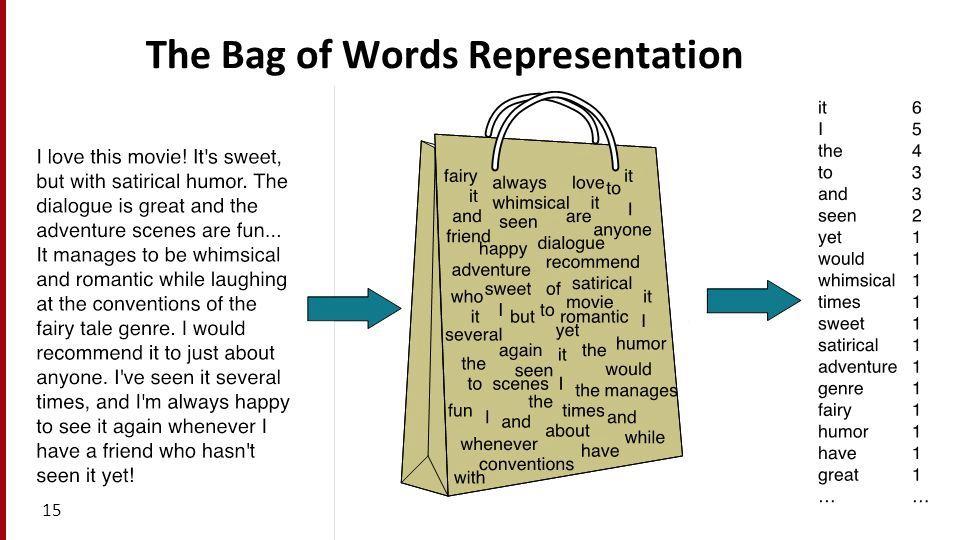
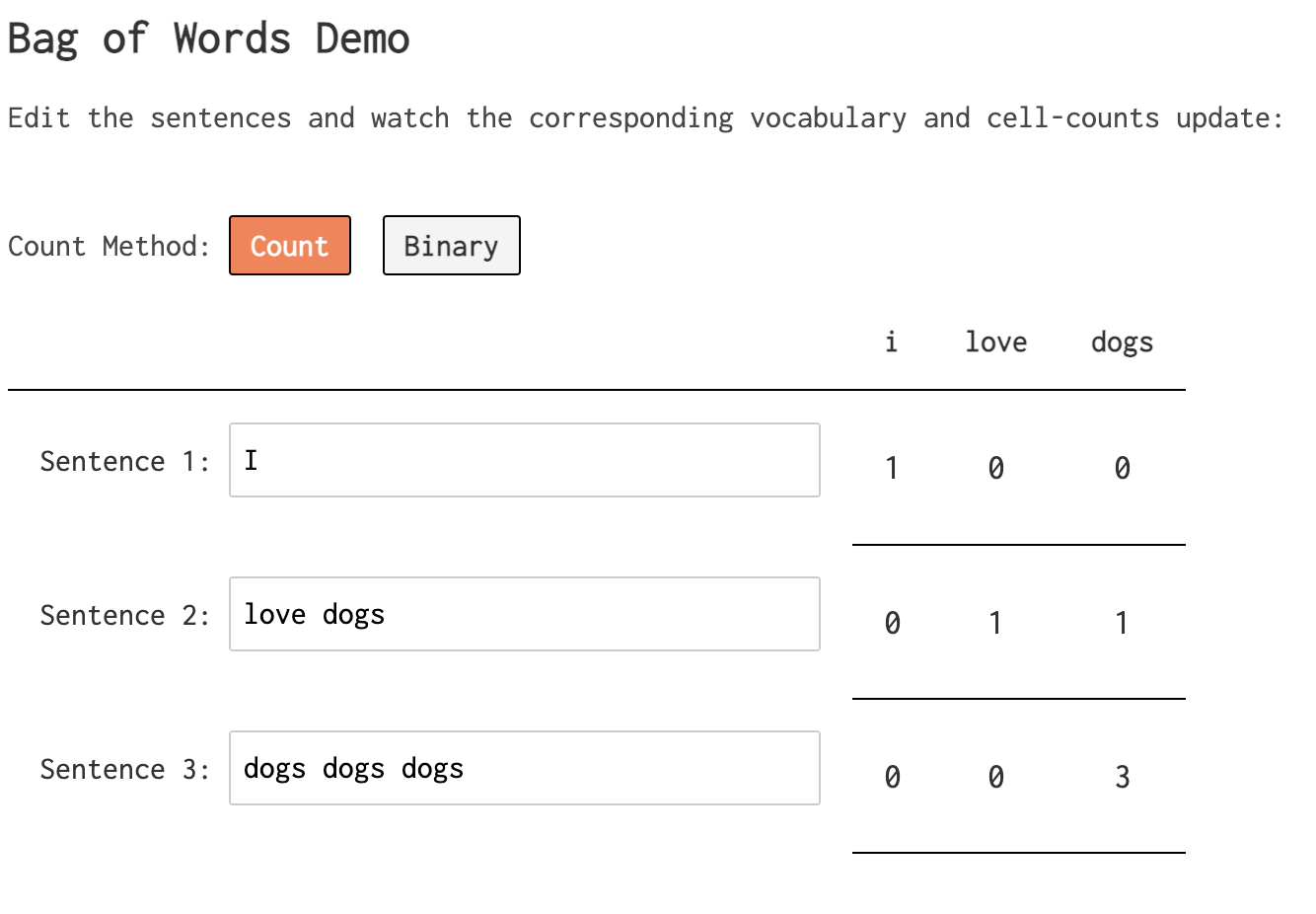
Bag of words 💰

---

Counting frequencies

• Idea: The most important terms in a document are the terms that occur most often.

• So, let's count the number of occurrences of each term in each document.
  In other words, let's count the frequency of each term in each document.

• For example, consider the following three documents:

big big big big data class
data big data science
science big data

• Let's construct a matrix, where:
  • there is one row per document,
  • one column per unique term, and
  • the value in row $d$ and column $t$ is the number of occurrences of term $t$ in document $d$.

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

Bag of words

• The bag of words model represents documents as vectors of word counts, i.e. term frequencies.
  The matrix below was created using the bag of words model.

• Each row in the bag of words matrix is a vector representation of a document.

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• For example, we can represent the document 2, data big data science, with the vector $\vec{d_2}$:

$$\vec{d_2} = \begin{bmatrix} 1 \\ 2 \\ 0 \\ 1 \end{bmatrix}$$

(source)
It is called "bag of words" because it doesn't consider order.

Aside: Interactive bag of words demo

Check this site out – it automatically generates a bag of words matrix for you!

(source)

Applications of the bag of words model

• Now that we have a matrix of word counts, what can we do with it?

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• Application: We could interpret the term with the largest value – that is, the most frequent term – in each document as being the most important.
  This is imperfect. What if a document has the term "the" as its most frequent term?

• Application: We could use the vector representations of documents to measure the similarity of two documents.
  This would enable us to find, for example, the SOTU speeches that are most similar to one another!

Recall: The dot product

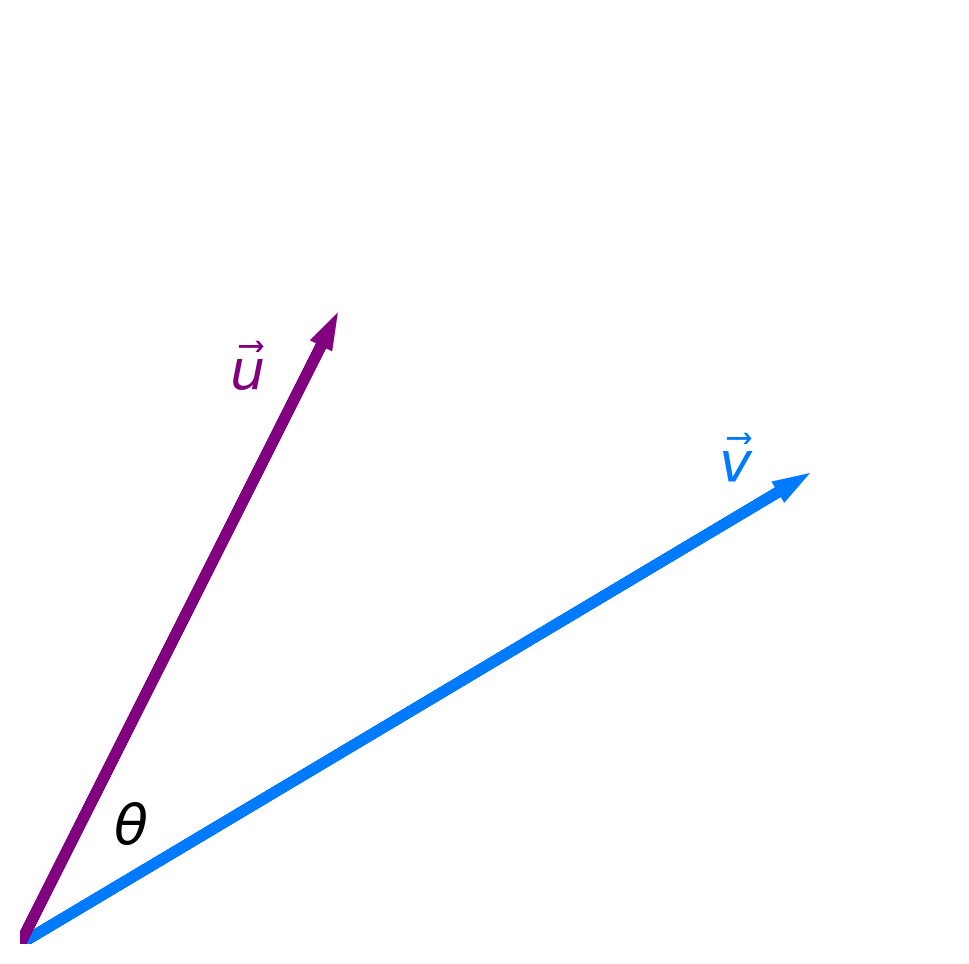
$$\require{color}$$

• Recall, if $\color{purple} \vec{u} = \begin{bmatrix} u_1 \\ u_2 \\ ... \\ u_n \end{bmatrix}$ and $\color{#007aff} \vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ ... \\ v_n \end{bmatrix}$ are two vectors, then their dot product ${\color{purple}\vec{u}} \cdot {\color{#007aff}\vec{v}}$ is defined as:

$${\color{purple}\vec{u}} \cdot {\color{#007aff}\vec{v}} = \sum_{i = 1}^n {\color{purple}u_i} {\color{#007aff} v_i} = {\color{purple}u_1} {\color{#007aff} v_1} + {\color{purple}u_2} {\color{#007aff} v_2} + ... + {\color{purple}u_n} {\color{#007aff} v_n}$$

• The dot product also has an equivalent geometric definition, which says that:

$${\color{purple}\vec{u}} \cdot {\color{#007aff}\vec{v}} = \lVert {\color{purple}\vec{u}} \rVert \lVert {\color{#007aff}\vec{v}} \rVert \cos \theta$$where $\theta$ is the angle between $\color{purple}\vec{u}$ and ${\color{#007aff}\vec{v}}$, and
$\lVert {\color{purple}\vec{u}} \rVert = \sqrt{{\color{purple} u_1}^2 + {\color{purple} u_2}^2 + ... + {\color{purple} u_n}^2}$
is the length of $\color{purple} \vec u$.

• The two definitions are equivalent! This equivalence allows us to find the angle $\theta$ between two vectors.

• For review, see LARDS, Section 2.

Angles and similarity

• Key idea: The more similar two vectors are, the smaller the angle $\theta$ between them is.

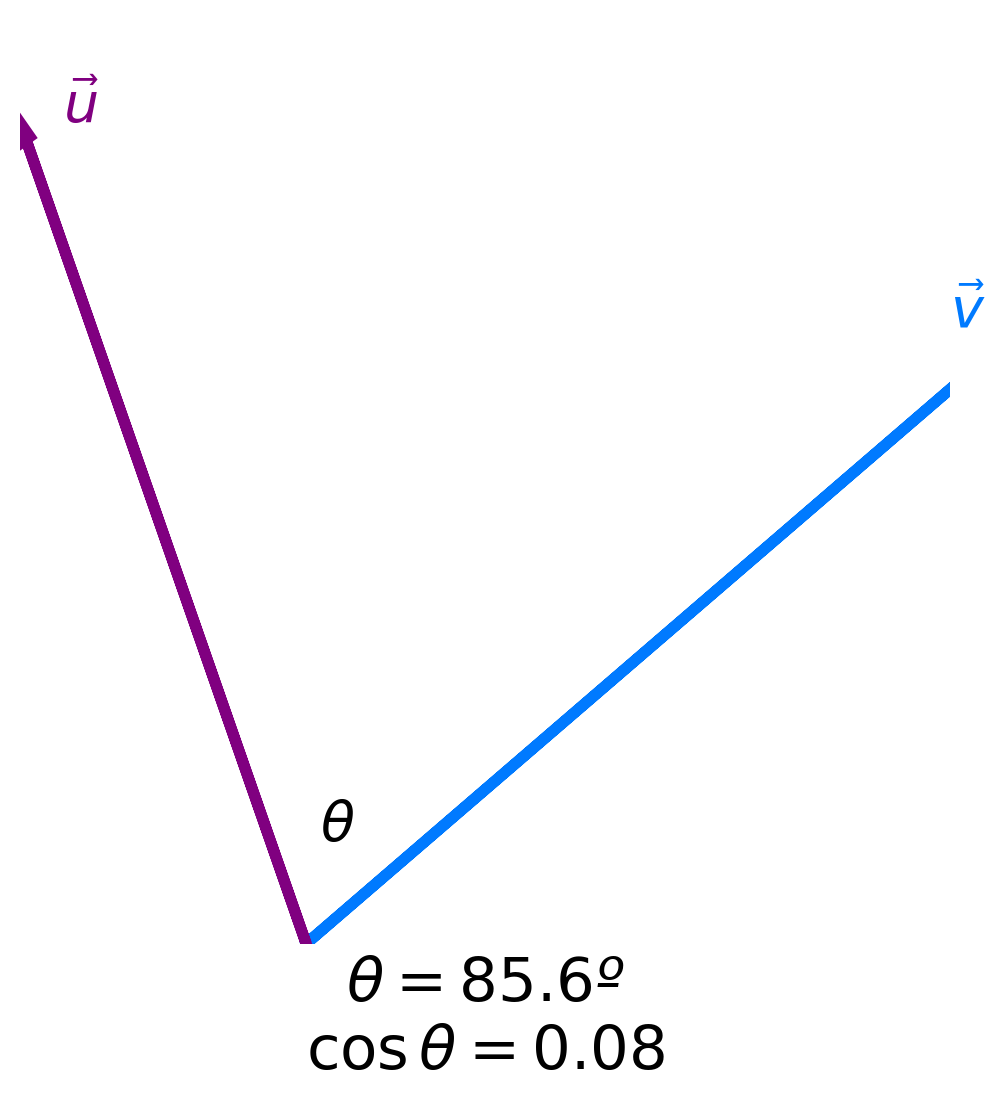
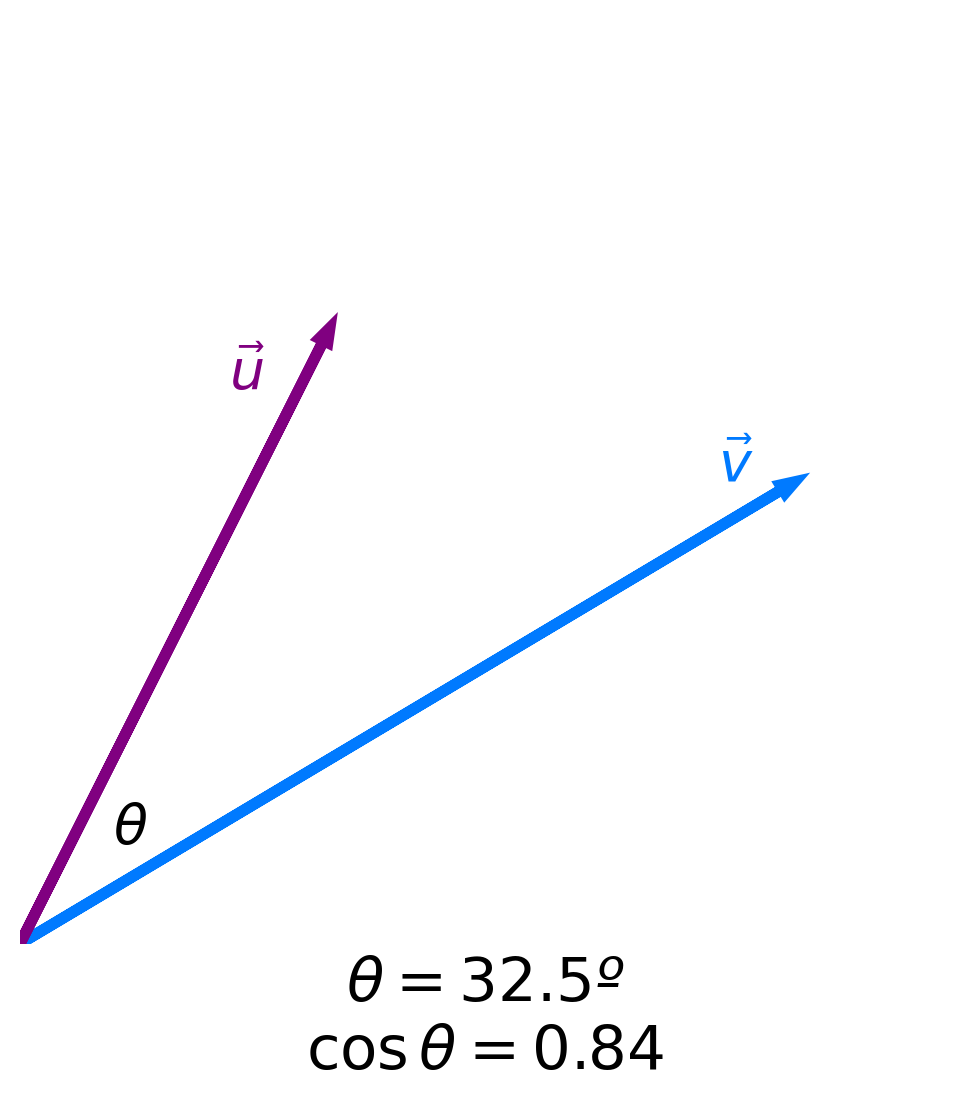
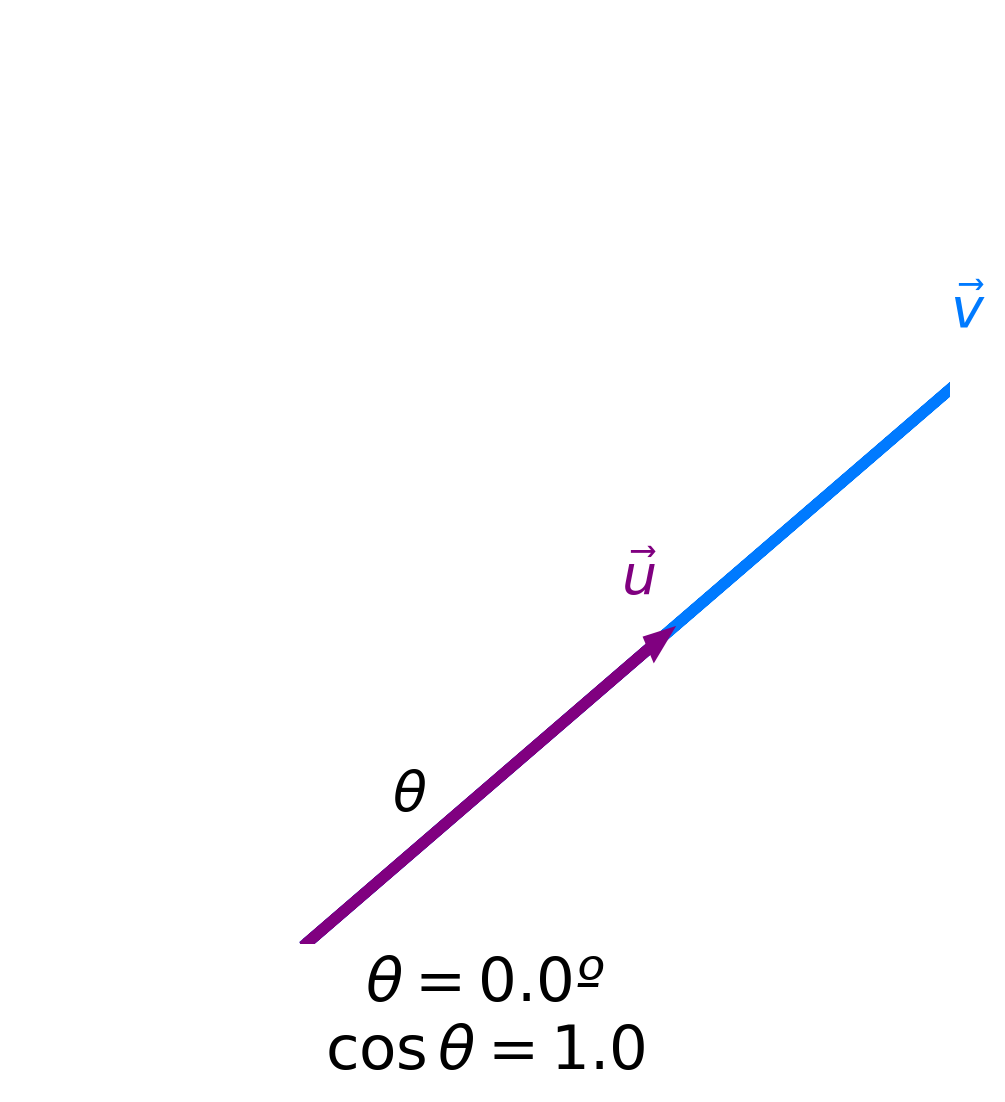
• The smaller the angle $\theta$ between two vectors is, the larger $\cos \theta$ is.

• The maximum value of $\cos \theta$ is 1, achieved when $\theta = 0$.

• Key idea: The more similar two vectors are, the larger $\cos \theta$ is!

Cosine similarity

• To measure the similarity between two documents, we can compute the cosine similarity of their vector representations:

$$\text{cosine similarity}(\vec u, \vec v) = \cos \theta = \boxed{\frac{\vec{u} \cdot \vec{v}}{|\vec{u}| | \vec{v}|}}$$

• If all elements in $\vec{u}$ and $\vec{v}$ are non-negative, then $\cos \theta$ ranges from 0 to 1.

• Key idea: The more similar two vectors are, the larger $\cos \theta$ is!

• Given a collection of documents, to find the most similiar pair, we can:
  1. Find the vector representation of each document.
  2. Find the cosine similarity of each pair of vectors.
  3. Return the documents whose vectors had the largest cosine similarity.

Activity

Consider the matrix of word counts we found earlier, using the bag of words model:

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

1. Which two documents have the highest dot product?
2. Which two documents have the highest cosine similarity?

Normalizing

• Why can't we just use the dot product – that is, why must we divide by $|\vec{u}| | \vec{v}|$ when computing cosine similarity?

$$\text{cosine similarity}(\vec u, \vec v) = \cos \theta = \boxed{\frac{\vec{u} \cdot \vec{v}}{|\vec{u}| | \vec{v}|}}$$

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• Consider the following two pairs of documents:

Pair	Dot Product	Cosine Similarity
big big big big data class and data big data science	6	0.577
science big data and data big data science	4	0.943

• "big big big big data class" has a large dot product with "data big data science" just because the former has the term "big" four times. But intuitively, "data big data science" and "science big data" should be much more similar, since they have almost the exact same terms.

• So, make sure to compute the cosine similarity – don't just use the dot product!
  If you don't normalize by the lengths of the vectors, documents with more terms will have artificially high similarities with other documents.

Reference Slide

Cosine distance

• Sometimes, you will see the cosine distance being used. It is the complement of cosine similarity:

$$\text{dist}(\vec{u}, \vec{v}) = 1 - \text{cosine similarity}(\vec u, \vec v) = 1 - \cos \theta$$

• If $\text{dist}(\vec{u}, \vec{v})$ is small, the two vector representations are similar.

Issues with the bag of words model

• Recall, the bag of words model encodes a document as a vector containing word frequencies.

• It doesn't consider the order of the terms.

"big data science" and "data science big" have the same vector representation, but mean different things.

• It doesn't consider the meaning of terms.
  "I really really hate data" and "I really really love data" have nearly identical vector representations, but very different meanings.

• It treats all words as being equally important. This is the issue we'll address today.
  In "I am a student" and "I am a teacher", it's clear to us humans that the most important terms are "student" and "teacher", respectively. But in the bag of words model, "student" and "I" appear the same number of times in the first document.

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

What questions do you have?

TF-IDF

---

What makes a word important?

• Issue: The bag of words model doesn't know which terms are "important" in a document.

• Consider the following document:

"my brother has a friend named billy who has an uncle named billy"

• "has" and "billy" both appear the same number of times in the document above. But "has" is an extremely common term overall, while "billy" isn't.

• Observation: If a term is important in a document, it will appear frequently in that document but not frequently in other documents.
  Let's try and find a way of giving scores to terms that keeps this in mind. If we can do this, then the terms with the highest scores can be used to summarize the document!

Term frequency

• The term frequency of a term $t$ in a document $d$, denoted $\text{tf}(t, d)$, is the proportion of words in document $d$ that are equal to $t$.

$$\text{tf}(t, d) = \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}$$

• Example: What is the term frequency of "billy" in the following document?

"my brother has a friend named billy who has an uncle named billy"

• Answer: $\frac{2}{13}$.

• Intuition: Terms that occur often within a document are important to the document's meaning.

$$\text{tf}(t, d) \text{ large} \implies t \text{ occurs often in $d$} \\ \text{tf}(t, d) \text{ small} \implies t \text{ occurs rarely in $d$}$$

• Issue: "has" also has a TF of $\frac{2}{13}$, but it seems less important than "billy".

Inverse document frequency

• The inverse document frequency of a term $t$ in a set of documents $d_1, d_2, ...$ is:

$$\text{idf}(t) = \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right)$$

• Example: What is the inverse document frequency of "billy" in the following three documents?
  • "my brother has a friend named billy who has an uncle named billy"
  • "my favorite artist is named jilly boel"
  • "why does he talk about someone named billy so often"

• Answer: $\log \left(\frac{3}{2}\right) \approx 0.4055$.
  Here, we used the natural logarithm. It doesn't matter which log base we use, as long as we keep it consistent throughout all of our calculations.

• Intuition: If a word appears in every document (like "the" or "has"), it is probably not a good summary of any one document.

• Think of $\text{idf}(t)$ as the "rarity factor" of $t$ across documents – the larger $\text{idf}(t)$ is, the more rare $t$ is.

$$\text{idf}(t) \text{ large} \implies t \text{ rare across all documents} \\ \text{idf}(t) \text{ small} \implies t \text{ common across all documents}$$

Intuition

• Goal: Measure how important term $t$ is to document $d$.
  Equivalent goal: Find the terms that best summarize $d$.

$$\text{tf}(t, d) = \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}$$$$\text{idf}(t) = \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right)$$

• If $\text{tf}(t, d)$ is small, then $t$ doesn't occur very often in $d$, so $t$ can't be very important to $d$.

• If $\text{idf}(t)$ is small, then $t$ occurs often amongst all documents, and so it can't be very important to $d$ specifically.

• If $\text{tf}(t, d)$ and $\text{idf}(t)$ are both large, then $t$ occurs often in $d$ but rarely overall. This makes $t$ important to $d$, i.e. a good "summary" of $d$.

Term frequency-inverse document frequency

• The term frequency-inverse document frequency (TF-IDF) of term $t$ in document $d$ is the product:

$$ \begin{align*}\text{tfidf}(t, d) &= \text{tf}(t, d) \cdot \text{idf}(t) \\\ &= \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right) \end{align*} $$

• If $\text{tfidf}(t, d)$ is large, then $t$ is important to $d$, because $t$ occurs often in $d$ but rarely across all documents.
  This means $t$ is a good summary of $d$!

• Note: TF-IDF is a heuristic method – there's no "proof" that it performs well.

• To know if $\text{tfidf}(t, d)$ is large for one particular term $t$, we need to compare it to $\text{tfidf}(t_i, d)$, for several different terms $t_i$.

Computing TF-IDF

• Question: What is the TF-IDF of "science" in "data big data science"?

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• Answer:

$$\begin{align*}\text{tfidf}(t, d) &= \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right) \\ &= \frac{1}{4} \cdot \log\left( \frac{3}{2} \right)\end{align*} $$

• Question: Is this big or small? Is "science" the best summary of "data big data science"?

TF-IDF of all terms in all documents

• On its own, the TF-IDF of one term in one document doesn't really tell us anything. We must compare it to TF-IDFs of other terms in that same document.

• Let's start with a DataFrame version of our bag of words matrix. It already contains the numerators for term frequency, i.e. $\text{tf}(t, d) = \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}$.

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

bow = pd.DataFrame([[4, 1, 1, 0], [1, 2, 0, 1], [1, 1, 0, 1]],
                   index=['big big big big data class', 'data big data science', 'science big data'],
                   columns=['big', 'data', 'class', 'science'])
bow

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• To convert the term counts to term frequencies, we'll divide by the sum of each row.
  Each row corresponds to the terms in one document; the sum of a row is the total number of terms in the document, which is the denominator in $\text{tf}(t, d) = \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}$.

# Verify that each row sums to 1!
tfs = bow.apply(lambda s: s / s.sum(), axis=1) 
tfs

	big	data	class	science
big big big big data class	0.67	0.17	0.17	0.00
data big data science	0.25	0.50	0.00	0.25
science big data	0.33	0.33	0.00	0.33

• Next, we need to find the inverse document frequency of each term, $t$, where $\text{idf}(t) = \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right)$.

def idf(term):
    term_column = tfs[term]
    return np.log(term_column.shape[0] / (term_column > 0).sum())

idf('class') == np.log(3 / 1)

True

all_idfs = [idf(c) for c in tfs.columns] 
all_idfs

[0.0, 0.0, 1.0986122886681098, 0.4054651081081644]

all_idfs = pd.Series(all_idfs, index=tfs.columns)
all_idfs

big        0.00
data       0.00
class      1.10
science    0.41
dtype: float64

• Finally, let's multiply tfs, the DataFrame with the term frequencies of each term in each document, by all_idfs, the Series of inverse document frequencies of each term.

tfidfs = tfs * all_idfs 
tfidfs

	big	data	class	science
big big big big data class	0.0	0.0	0.18	0.00
data big data science	0.0	0.0	0.00	0.10
science big data	0.0	0.0	0.00	0.14

Interpreting TF-IDFs

tfidfs

	big	data	class	science
big big big big data class	0.0	0.0	0.18	0.00
data big data science	0.0	0.0	0.00	0.10
science big data	0.0	0.0	0.00	0.14

• The TF-IDF of 'class' in the first sentence is $\approx 0.18$.

• The TF-IDF of 'data' in the second sentence is 0.

• Note that there are two ways that $\text{tfidf}(t, d) = \text{tf}(t, d) \cdot \text{idf}(t)$ can be 0:
  • If $t$ appears in every document, because then $\text{idf}(t) = \log (\frac{\text{# documents}}{\text{# documents}}) = \log(1) = 0$.
  • If $t$ does not appear in document $d$, because then $\text{tf}(t, d) = \frac{0}{\text{len}(d)} = 0$.

• The term that best summarizes a document is the term with the highest TF-IDF for that document:

tfidfs.idxmax(axis=1) 

big big big big data class      class
data big data science         science
science big data              science
dtype: object

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

What questions do you have?

Example: State of the Union addresses 🎤

---

Overview

• Now that we have a robust technique for assigning scores to terms – that is, TF-IDF – we can use it to find the most important terms in each State of the Union address.

speeches

	text
George Washington: January 8, 1790	fellow citizens of the senate and house of re...
George Washington: December 8, 1790	fellow citizens of the senate and house of re...
George Washington: October 25, 1791	fellow citizens of the senate and house of re...
...	...
Joseph R. Biden Jr.: March 1, 2022	madam speaker madam vice president and our ...
Joseph R. Biden Jr.: February 7, 2023	mr speaker madam vice president our firs...
Joseph R. Biden Jr.: March 7, 2024	good evening mr speaker madam vice presi...

234 rows × 1 columns

• To recap, we'll need to compute:

        for each term t:
            for each speech d:
                compute tfidf(t, d)

• This time, we don't already have a bag of words matrix, so we'll need to start from scratch.

Finding all unique terms

• First, we need to find the unique terms used across all SOTU speeches.
  These words will form the columns of our TF-IDF matrix.

all_unique_terms = speeches['text'].str.split().explode().value_counts() # Faster than .sum() from last lecture! 
all_unique_terms

text
the        147338
of          94505
to          60827
            ...  
palacio         1
not'            1
isn             1
Name: count, Length: 24259, dtype: int64

• Since there are over 20,000 unique terms, our future calculations will otherwise take too much time to run. Let's take the 500 most frequent, across all speeches, for speed.

unique_terms = all_unique_terms.iloc[:500].index 
unique_terms

Index(['the', 'of', 'to', 'and', 'in', 'a', 'that', 'for', 'be', 'our',
       ...
       'months', 'call', 'increasing', 'desire', 'submitted', 'throughout',
       'point', 'trust', 'set', 'object'],
      dtype='object', name='text', length=500)

Finding term frequencies

• Next, let's find the bag of words matrix, i.e. a matrix that tells us the number of occurrences of each term in each document.

• What's the difference between the following two expressions?

speeches['text'].str.count('the')

George Washington: January 8, 1790       120
George Washington: December 8, 1790      160
George Washington: October 25, 1791      302
                                        ... 
Joseph R. Biden Jr.: March 1, 2022       514
Joseph R. Biden Jr.: February 7, 2023    507
Joseph R. Biden Jr.: March 7, 2024       398
Name: text, Length: 234, dtype: int64

# Remember, the \b special character matches **word boundaries**!
# This makes sure that we don't count instances of "the" that are part of other words,
# like "thesaurus".
speeches['text'].str.count(r'\bthe\b')

George Washington: January 8, 1790        97
George Washington: December 8, 1790      122
George Washington: October 25, 1791      242
                                        ... 
Joseph R. Biden Jr.: March 1, 2022       357
Joseph R. Biden Jr.: February 7, 2023    338
Joseph R. Biden Jr.: March 7, 2024       296
Name: text, Length: 234, dtype: int64

• Let's repeat the above calculation for every unique term. This code will take a while to run, so we'll use the tdqm package to track its progress.
  Install with mamba install tqdm if needed.

from tqdm.notebook import tqdm
counts_dict = {}
for term in tqdm(unique_terms):
    counts_dict[term] = speeches['text'].str.count(fr'\b{term}\b')        
counts = pd.DataFrame(counts_dict, index=speeches.index)
counts

	the	of	to	and	...	point	trust	set	object
George Washington: January 8, 1790	97	69	56	41	...	0	1	0	3
George Washington: December 8, 1790	122	89	49	45	...	0	0	0	2
George Washington: October 25, 1791	242	159	88	73	...	0	2	2	2
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: March 1, 2022	357	189	272	316	...	3	3	3	0
Joseph R. Biden Jr.: February 7, 2023	338	166	261	232	...	1	6	0	0
Joseph R. Biden Jr.: March 7, 2024	296	132	216	234	...	1	2	1	0

234 rows × 500 columns

• The above DataFrame does not contain term frequencies. To convert the values above to term frequencies, we need to normalize by the sum of each row.

tfs = counts.apply(lambda s: s / s.sum(), axis=1)
tfs

	the	of	to	and	...	point	trust	set	object
George Washington: January 8, 1790	0.12	0.09	0.07	0.05	...	0.00e+00	1.24e-03	0.00e+00	3.73e-03
George Washington: December 8, 1790	0.12	0.09	0.05	0.04	...	0.00e+00	0.00e+00	0.00e+00	1.97e-03
George Washington: October 25, 1791	0.15	0.10	0.05	0.04	...	0.00e+00	1.20e-03	1.20e-03	1.20e-03
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: March 1, 2022	0.07	0.04	0.05	0.06	...	5.87e-04	5.87e-04	5.87e-04	0.00e+00
Joseph R. Biden Jr.: February 7, 2023	0.07	0.04	0.06	0.05	...	2.12e-04	1.27e-03	0.00e+00	0.00e+00
Joseph R. Biden Jr.: March 7, 2024	0.07	0.03	0.05	0.06	...	2.37e-04	4.74e-04	2.37e-04	0.00e+00

234 rows × 500 columns

Finding TF-IDFs

• Finally, we'll need to find the inverse document frequencies (IDF) of each term.

• Using apply, we can find the IDFs of each term and multiply them by the term frequencies in one step.

$$\begin{align*}\text{tfidf}(t, d) &= \underbrace{\frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}}_{\text{we already computed these}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right)\end{align*} $$

tfidfs = tfs.apply(lambda s: s * np.log(s.shape[0] / (s > 0).sum())) 
tfidfs

	the	of	to	and	...	point	trust	set	object
George Washington: January 8, 1790	0.0	0.0	0.0	0.0	...	0.00e+00	5.78e-04	0.00e+00	2.78e-03
George Washington: December 8, 1790	0.0	0.0	0.0	0.0	...	0.00e+00	0.00e+00	0.00e+00	1.47e-03
George Washington: October 25, 1791	0.0	0.0	0.0	0.0	...	0.00e+00	5.58e-04	4.79e-04	8.95e-04
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: March 1, 2022	0.0	0.0	0.0	0.0	...	2.27e-04	2.73e-04	2.34e-04	0.00e+00
Joseph R. Biden Jr.: February 7, 2023	0.0	0.0	0.0	0.0	...	8.19e-05	5.91e-04	0.00e+00	0.00e+00
Joseph R. Biden Jr.: March 7, 2024	0.0	0.0	0.0	0.0	...	9.16e-05	2.20e-04	9.46e-05	0.00e+00

234 rows × 500 columns

• Why are the TF-IDFs of many common words 0?

Summarizing speeches

• By using idxmax, we can find the term with the highest TF-IDF in each speech.

summaries = tfidfs.idxmax(axis=1) 
summaries

George Washington: January 8, 1790           object
George Washington: December 8, 1790      convention
George Washington: October 25, 1791       provision
                                            ...    
Joseph R. Biden Jr.: March 1, 2022          tonight
Joseph R. Biden Jr.: February 7, 2023       tonight
Joseph R. Biden Jr.: March 7, 2024          tonight
Length: 234, dtype: object

• What if we want to see the 5 terms with the highest TF-IDFs, for each speech?

def five_largest(row):
    return ', '.join(row.index[row.argsort()][-5:])

keywords = tfidfs.apply(five_largest, axis=1).to_frame().rename(columns={0: 'most important terms'})
keywords

	most important terms
George Washington: January 8, 1790	your, proper, regard, ought, object
George Washington: December 8, 1790	case, established, object, commerce, convention
George Washington: October 25, 1791	community, upon, lands, proper, provision
...	...
Joseph R. Biden Jr.: March 1, 2022	let, jobs, americans, get, tonight
Joseph R. Biden Jr.: February 7, 2023	down, percent, let, jobs, tonight
Joseph R. Biden Jr.: March 7, 2024	jobs, down, get, americans, tonight

234 rows × 1 columns

• Uncomment the cell below to see every single row of keywords.
  Cool!

# display_df(keywords, rows=234)

Cosine similarity, revisited

• Each row of tfidfs contains a vector representation of a speech. This means that we can compute the cosine similarities between any two speeches!
  The only difference now is that we used TF-IDF to find $\vec u$ and $\vec v$, rather than the bag of words model.

$$\text{cosine similarity}(\vec u, \vec v) = \frac{\vec{u} \cdot \vec{v}}{|\vec{u}| | \vec{v}|}$$

tfidfs

	the	of	to	and	...	point	trust	set	object
George Washington: January 8, 1790	0.0	0.0	0.0	0.0	...	0.00e+00	5.78e-04	0.00e+00	2.78e-03
George Washington: December 8, 1790	0.0	0.0	0.0	0.0	...	0.00e+00	0.00e+00	0.00e+00	1.47e-03
George Washington: October 25, 1791	0.0	0.0	0.0	0.0	...	0.00e+00	5.58e-04	4.79e-04	8.95e-04
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: March 1, 2022	0.0	0.0	0.0	0.0	...	2.27e-04	2.73e-04	2.34e-04	0.00e+00
Joseph R. Biden Jr.: February 7, 2023	0.0	0.0	0.0	0.0	...	8.19e-05	5.91e-04	0.00e+00	0.00e+00
Joseph R. Biden Jr.: March 7, 2024	0.0	0.0	0.0	0.0	...	9.16e-05	2.20e-04	9.46e-05	0.00e+00

234 rows × 500 columns

def sim(speech_1, speech_2):
    v1 = tfidfs.loc[speech_1]
    v2 = tfidfs.loc[speech_2]
    return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))

sim('George Washington: January 8, 1790', 'George Washington: December 8, 1790')

0.5229932678775406

sim('George Washington: January 8, 1790', 'Joseph R. Biden Jr.: March 7, 2024')

0.0692680683399537

• We can also find the most similar pair of speeches:

from itertools import combinations

sims_dict = {}
# For every pair of speeches, find the similarity and store it in
# the sims_dict dictionary.
for pair in combinations(tfidfs.index, 2):
    sims_dict[pair] = sim(pair[0], pair[1])
# Turn the sims_dict dictionary into a DataFrame.
sims = (
    pd.Series(sims_dict)
    .reset_index()
    .rename(columns={'level_0': 'speech 1', 'level_1': 'speech 2', 0: 'cosine similarity'})
    .sort_values('cosine similarity', ascending=False)
)
sims

	speech 1	speech 2	cosine similarity
27171	Barack Obama: January 25, 2011	Barack Obama: February 12, 2013	0.93
11685	James Polk: December 8, 1846	James Polk: December 7, 1847	0.93
27183	Barack Obama: January 24, 2012	Barack Obama: February 12, 2013	0.92
...	...	...	...
6714	James Monroe: December 7, 1819	Ronald Reagan: January 26, 1982	0.04
18192	Grover Cleveland: December 6, 1887	George W. Bush: September 20, 2001	0.04
6733	James Monroe: December 7, 1819	George W. Bush: February 27, 2001	0.03

27261 rows × 3 columns

• For instance, we can find the most similar pairs of speeches by different Presidents:

sims[sims['speech 1'].str.split(':').str[0] != sims['speech 2'].str.split(':').str[0]]

	speech 1	speech 2	cosine similarity
27191	Barack Obama: January 24, 2012	Joseph R. Biden Jr.: April 28, 2021	0.88
27239	Donald J. Trump: February 27, 2017	Joseph R. Biden Jr.: March 7, 2024	0.87
27243	Donald J. Trump: January 30, 2018	Joseph R. Biden Jr.: March 1, 2022	0.87
...	...	...	...
6714	James Monroe: December 7, 1819	Ronald Reagan: January 26, 1982	0.04
18192	Grover Cleveland: December 6, 1887	George W. Bush: September 20, 2001	0.04
6733	James Monroe: December 7, 1819	George W. Bush: February 27, 2001	0.03

26624 rows × 3 columns

Aside: What if we remove the $\log$ from $\text{idf}(t)$?

• Let's try it and see what happens.
  Below is another, quicker implementation of how we might find TF-IDFs.

tfidfs_nl_dict = {}
tf_denom = speeches['text'].str.split().str.len()
for word in tqdm(unique_terms):
    re_pat = fr' {word} ' # Imperfect pattern for speed.
    tf = speeches['text'].str.count(re_pat) / tf_denom
    idf_nl = len(speeches) / speeches['text'].str.contains(re_pat).sum()
    tfidfs_nl_dict[word] =  tf * idf_nl

tfidfs_nl = pd.DataFrame(tfidfs_nl_dict)
tfidfs_nl.head()

	the	of	to	and	...	point	trust	set	object
George Washington: January 8, 1790	0.09	0.06	0.05	0.04	...	0.0	1.46e-03	0.00e+00	5.81e-03
George Washington: December 8, 1790	0.09	0.06	0.03	0.03	...	0.0	0.00e+00	0.00e+00	3.01e-03
George Washington: October 25, 1791	0.11	0.07	0.04	0.03	...	0.0	1.38e-03	1.29e-03	1.83e-03
George Washington: November 6, 1792	0.09	0.07	0.04	0.03	...	0.0	2.28e-03	0.00e+00	2.02e-03
George Washington: December 3, 1793	0.09	0.07	0.04	0.02	...	0.0	8.10e-04	0.00e+00	1.07e-03

5 rows × 500 columns

keywords_nl = tfidfs_nl.apply(five_largest, axis=1)
keywords_nl

George Washington: January 8, 1790        a, and, to, of, the
George Washington: December 8, 1790      in, and, to, of, the
George Washington: October 25, 1791       a, and, to, of, the
                                                 ...         
Joseph R. Biden Jr.: March 1, 2022       we, of, to, and, the
Joseph R. Biden Jr.: February 7, 2023     a, of, and, to, the
Joseph R. Biden Jr.: March 7, 2024        a, of, to, and, the
Length: 234, dtype: object

• What do you notice?

The role of $\log$ in $\text{idf}(t)$

$$ \begin{align*}\text{tfidf}(t, d) &= \text{tf}(t, d) \cdot \text{idf}(t) \\\ &= \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right) \end{align*} $$

• Remember, for any positive input $x$, $\log(x)$ is (much) smaller than $x$.

• In $\text{idf}(t)$, the $\log$ "dampens" the impact of the ratio $\frac{\text{# documents}}{\text{# documents with $t$}}$. If a word is very common, the ratio will be close to 1. The log of the ratio will be close to 0.

(1000 / 999)

1.001001001001001

np.log(1000 / 999)

0.001000500333583622

• If a word is very common (e.g. "the"), and we didn't have the $\log$, we'd be multiplying the term frequency by a large factor.

• If a word is very rare, the ratio $\frac{\text{# documents}}{\text{# documents with $t$}}$ will be very large. However, for instance, a word being seen in 2 out of 50 documents is not very different than being seen in 2 out of 500 documents (it is very rare in both cases), and so $\text{idf}(t)$ should be similar in both cases.

(50 / 2)

25.0

(500 / 2)

250.0

np.log(50 / 2)

3.2188758248682006

np.log(500 / 2)

5.521460917862246

Activity

This is an old exam question!

Nishant decides to look at reviews for the Catamaran Resort Hotel and Spa. TripAdvisor has 96 reviews for the hotel; of those 96, Nishant’s favorite review was:

"close to the beach but far from the beach beach"

1. What is the TF of "beach" in Nishant’s favorite review? Give your answer as a simplified fraction.
2. The TF-IDF of "beach" in Nishant’s favorite review is $\frac{9}{10}$, when using a base-2 logarithm to compute the IDF. How many of the reviews on TripAdvisor for this hotel contain the term "beach"?

TF-IDF, implemented

• In Homework 6, we may ask you to implement TF-IDF to further your own understanding.

• But, in practical projects, you'd use an existing implementation of it, like TfIdfVectorizer in sklearn.
  See the documentation for more details.

from sklearn.feature_extraction.text import TfidfVectorizer

vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(speeches['text'])
tfidfs_sklearn = pd.DataFrame(X.toarray(), 
                              columns=vectorizer.get_feature_names_out(), 
                              index=speeches.index)

tfidfs_sklearn

	aaa	aaron	abandon	abandoned	...	zones	zoological	zooming	zuloaga
George Washington: January 8, 1790	0.0	0.0	0.00e+00	0.0	...	0.0	0.0	0.0	0.0
George Washington: December 8, 1790	0.0	0.0	0.00e+00	0.0	...	0.0	0.0	0.0	0.0
George Washington: October 25, 1791	0.0	0.0	0.00e+00	0.0	...	0.0	0.0	0.0	0.0
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: March 1, 2022	0.0	0.0	2.97e-03	0.0	...	0.0	0.0	0.0	0.0
Joseph R. Biden Jr.: February 7, 2023	0.0	0.0	0.00e+00	0.0	...	0.0	0.0	0.0	0.0
Joseph R. Biden Jr.: March 7, 2024	0.0	0.0	0.00e+00	0.0	...	0.0	0.0	0.0	0.0

234 rows × 23739 columns

tfidfs_sklearn[tfidfs_sklearn['zuloaga'] != 0]

	aaa	aaron	abandon	abandoned	...	zones	zoological	zooming	zuloaga
James Buchanan: December 19, 1859	0.0	0.0	0.0	0.00e+00	...	0.0	0.0	0.0	1.34e-02
James Buchanan: December 3, 1860	0.0	0.0	0.0	1.30e-03	...	0.0	0.0	0.0	2.91e-03

2 rows × 23739 columns

Summary

• One way to turn text, like 'big big big big data classs', into numbers, is to count the number of occurrences of each word in the document, ignoring order. This is done using the bag of words model.
• Term frequency-inverse document frequency (TF-IDF) is a statistic that tries to quantify how important a term (word) is to a document. It balances:
  • how often a term appears in a particular document, $\text{tf}(t, d)$, with
  • how often a term appears across documents, $\text{idf}(t)$.
  • For a given document, the word with the highest TF-IDF is thought to "best summarize" that document.
• Both the bag of words model and TF-IDF are ways of converting texts to vector representations.
• To measure the similarity of two texts, convert the texts to their vector representations, and use cosine similarity.