from lec_utils import *

Lecture 10

Text as Data

EECS 398: Practical Data Science, Spring 2025

practicaldsc.org • github.com/practicaldsc/sp25 • 📣 See latest announcements here on Ed

Agenda 📆

• From text to numbers.
• Bag of words 💰.
• TF-IDF.
• Example: State of the Union addresses 🎤.

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

From text to numbers

---

From text to numbers

• How do we represent a text document using numbers?

• Computers and mathematical formulas are designed to work with numbers, not words.

• So, if we can convert documents into numbers, we can:
  • summarize documents by finding their most important words (today).
  • quantify the similarity of two documents (today).
  • use a document as input in a regression or classification model (starting next lecture).

Example: State of the Union addresses 🎤

• Each year, the sitting US President delivers a "State of the Union" address.
  The 2025 State of the Union (SOTU) address was on March 4th, 2025.
  "Address" is another word for "speech."

from IPython.display import YouTubeVideo
YouTubeVideo('XkFKNkAEzQ8')

• The file 'data/stateoftheunion1790-2025.txt' contains the transcript of every SOTU address since 1790.
  Source: The American Presidency Project.

with open('data/stateoftheunion1790-2025.txt') as f:
    sotu = f.read()

# The file is over 10 million characters long!
len(sotu) / 1_000_000

10.675837

Terminology

• In text analysis, each piece of text we want to analyze is called a document.
  Here, each speech is a document.

• Documents are made up of terms, i.e. words.

• A collection of documents is called a corpus.
  Here, the corpus is the set of all SOTU speeches from 1790-2025.

Extracting speeches

• In the string sotu, each document is separated by '***'.

speeches_lst = sotu.split('\n***\n')[1:]
len(speeches_lst)

235

• Note that each "speech" currently contains other information, like the name of the president and the date of the address.

print(speeches_lst[-1][:1000])

Address Before a Joint Session of Congress 
Donald J. Trump
March 4, 2025

The President. Thank you. Thank you very much. Thank you very much. It's a great honor. Thank you very much.

Speaker Johnson, Vice President Vance, the First Lady of the United States, Members of the United States Congress: Thank you very much.

And to my fellow citizens, America is back.

Audience members. U.S.A.! U.S.A.! U.S.A.!

The President. Six weeks ago, I stood beneath the dome of this Capitol and proclaimed the dawn of the golden age of America. From that moment on, it has been nothing but swift and unrelenting action to usher in the greatest and most successful era in the history of our country.

We have accomplished more in 43 days than most administrations accomplished in 4 years or 8 years, and we are just getting started. [Applause] Thank you.

I return to this Chamber tonight to report that America's momentum is back, our spirit is back, our pride is back, our confidence is back, and the America

• Let's extract just the text of each speech and put it in a DataFrame.
  Along the way, we'll use our new knowledge of regular expressions to remove capitalization and punctuation, so we can just focus on the content itself.

def create_speeches_df(speeches_lst):
    def extract_struct(speech):
        L = speech.strip().split('\n', maxsplit=3)
        L[3] = re.sub(r"[^A-Za-z' ]", ' ', L[3]).lower() # Replaces anything OTHER than letters with ' '.
        L[3] = re.sub(r"it's", 'it is', L[3]).replace(' s ', '')
        return dict(zip(['president', 'date', 'text'], L[1:]))
    speeches = pd.DataFrame(list(map(extract_struct, speeches_lst)))
    speeches.index = speeches['president'].str.strip() + ': ' + speeches['date']
    speeches = speeches[['text']]
    return speeches

speeches = create_speeches_df(speeches_lst)
speeches

	text
George Washington: January 8, 1790	fellow citizens of the senate and house of re...
George Washington: December 8, 1790	fellow citizens of the senate and house of re...
George Washington: October 25, 1791	fellow citizens of the senate and house of re...
...	...
Joseph R. Biden Jr.: February 7, 2023	mr speaker madam vice president our firs...
Joseph R. Biden Jr.: March 7, 2024	good evening mr speaker madam vice presi...
Donald J. Trump: March 4, 2025	the president thank you thank you very much...

235 rows × 1 columns

Quantifying speeches

• Our goal is to produce a DataFrame that contains the most important terms in each speech, i.e. the terms that best summarize each speech:

	most important terms
George Washington: January 8, 1790	your, proper, regard, ought, object
George Washington: December 8, 1790	case, established, object, commerce, convention
...	...
Joseph R. Biden Jr.: February 7, 2023	americans, down, percent, jobs, tonight
Joseph R. Biden Jr.: March 7, 2024	jobs, down, get, americans, tonight

• To do so, we will need to come up with a way of assigning a numerical score to each term in each speech.
  We'll come up with a score for each term such that terms with higher scores are more important!

	jobs	down	commerce	...	convention	americans	tonight
George Washington: January 8, 1790	0.00e+00	0.00e+00	3.55e-04	...	0.00e+00	0.00e+00	0.00e+00
George Washington: December 8, 1790	0.00e+00	0.00e+00	1.10e-03	...	1.18e-03	0.00e+00	0.00e+00
...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: February 7, 2023	2.73e-03	1.78e-03	0.00e+00	...	0.00e+00	1.56e-03	3.34e-03
Joseph R. Biden Jr.: March 7, 2024	1.77e-03	1.96e-03	5.93e-05	...	0.00e+00	2.37e-03	3.90e-03

• In doing so, we will represent each speech as a vector.

Bag of words 💰

---

Counting frequencies

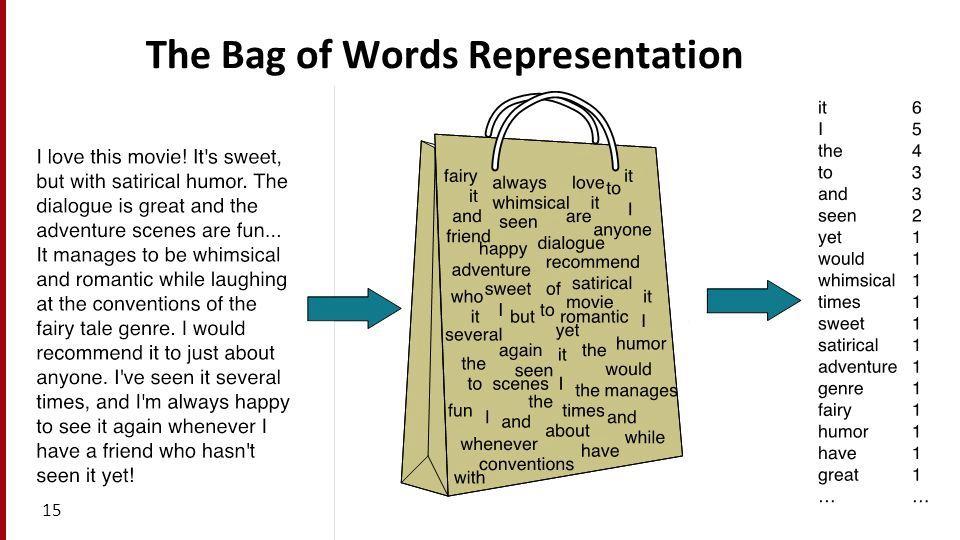
• Idea: The most important terms in a document are the terms that occur most often.

• So, let's count the number of occurrences of each term in each document.
  In other words, let's count the frequency of each term in each document.

• For example, consider the following three documents:

big big big big data class
data big data science
science big data

• Let's construct a matrix, where:
  • there is one row per document,
  • one column per unique term, and
  • the value in row $d$ and column $t$ is the number of occurrences of term $t$ in document $d$.

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

Bag of words

• The bag of words model represents documents as vectors of word counts, i.e. term frequencies.
  The matrix below was created using the bag of words model.

• Each row in the bag of words matrix is a vector representation of a document.

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• For example, we can represent the document 2, data big data science, with the vector $\vec{d_2}$:

$$\vec{d_2} = \begin{bmatrix} 1 \\ 2 \\ 0 \\ 1 \end{bmatrix}$$

(source)
It is called "bag of words" because it doesn't consider order.

Aside: Interactive bag of words demo

Check this site out – it automatically generates a bag of words matrix for you!

(source)

Applications of the bag of words model

• Now that we have a matrix of word counts, what can we do with it?

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• Application: We could interpret the term with the largest value – that is, the most frequent term – in each document as being the most important.
  This is imperfect. What if a document has the term "the" as its most frequent term?

• Application: We could use the vector representations of documents to measure the similarity of two documents.
  This would enable us to find, for example, the SOTU speeches that are most similar to one another!

Recall: The dot product

$$\require{color}$$

• Recall, if $\color{purple} \vec{u} = \begin{bmatrix} u_1 \\ u_2 \\ ... \\ u_n \end{bmatrix}$ and $\color{#007aff} \vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ ... \\ v_n \end{bmatrix}$ are two vectors, then their dot product ${\color{purple}\vec{u}} \cdot {\color{#007aff}\vec{v}}$ is defined as:

$${\color{purple}\vec{u}} \cdot {\color{#007aff}\vec{v}} = \sum_{i = 1}^n {\color{purple}u_i} {\color{#007aff} v_i} = {\color{purple}u_1} {\color{#007aff} v_1} + {\color{purple}u_2} {\color{#007aff} v_2} + ... + {\color{purple}u_n} {\color{#007aff} v_n}$$

• The dot product also has an equivalent geometric definition, which says that:

$${\color{purple}\vec{u}} \cdot {\color{#007aff}\vec{v}} = \lVert {\color{purple}\vec{u}} \rVert \lVert {\color{#007aff}\vec{v}} \rVert \cos \theta$$where $\theta$ is the angle between $\color{purple}\vec{u}$ and ${\color{#007aff}\vec{v}}$, and
$\lVert {\color{purple}\vec{u}} \rVert = \sqrt{{\color{purple} u_1}^2 + {\color{purple} u_2}^2 + ... + {\color{purple} u_n}^2}$
is the length of $\color{purple} \vec u$.

• The two definitions are equivalent! This equivalence allows us to find the angle $\theta$ between two vectors.

• For review, see the Linear Algebra Guides on the course website.

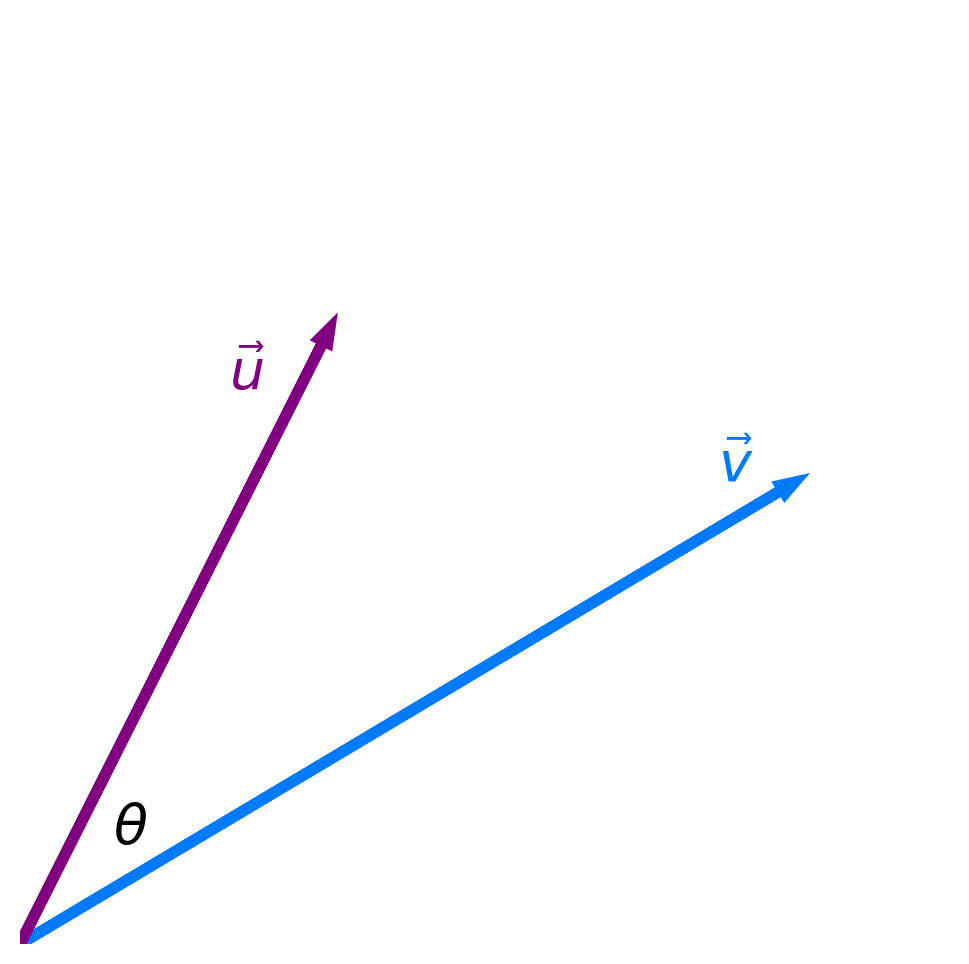
Angles and similarity

• Key idea: The more similar two vectors are, the smaller the angle $\theta$ between them is.

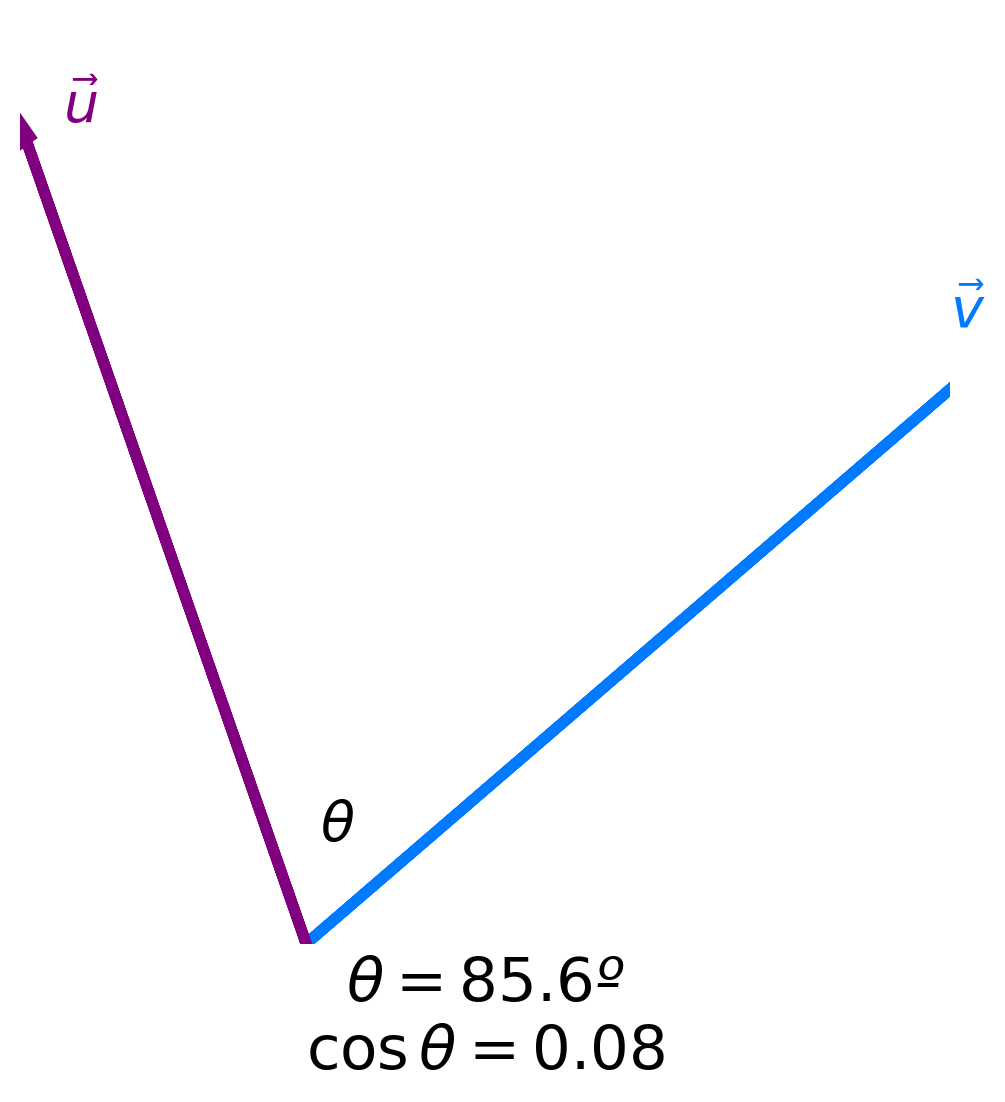
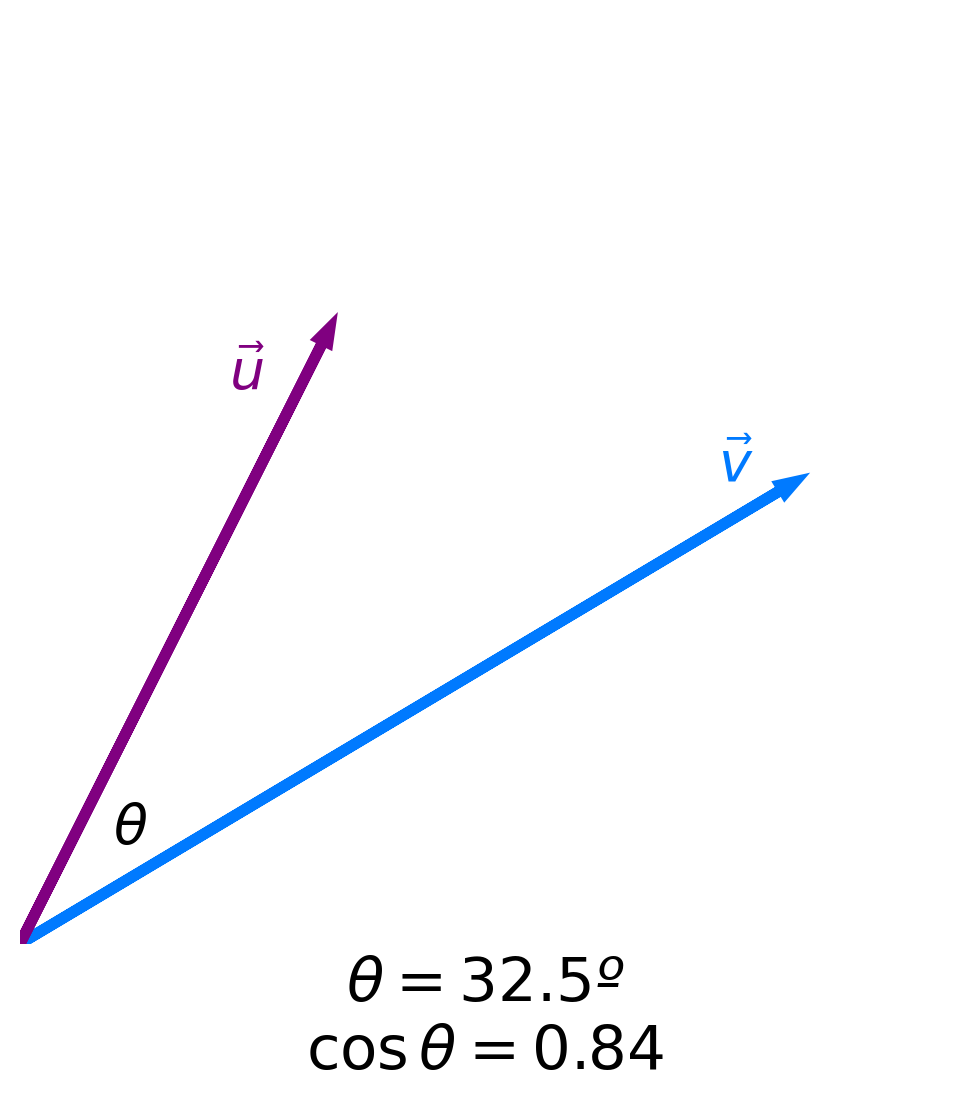
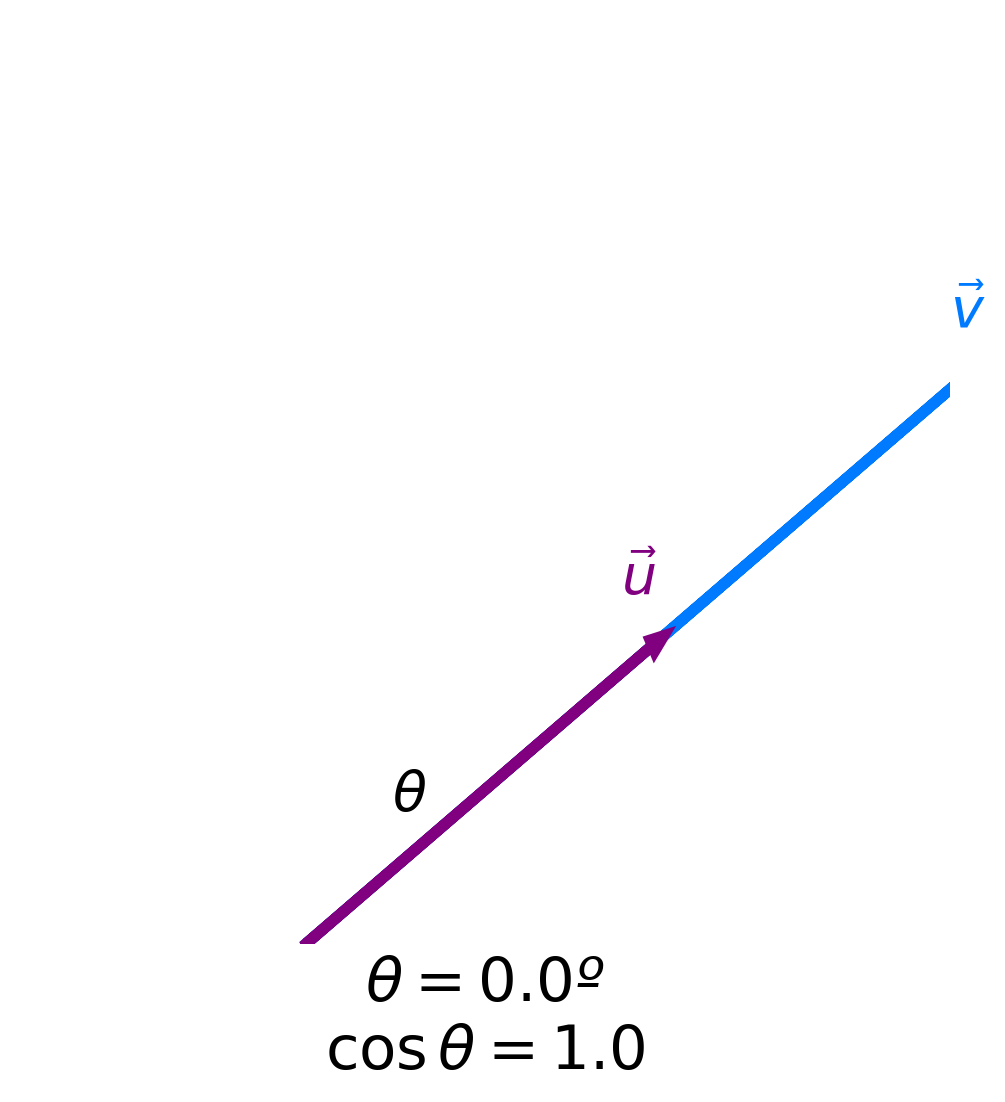
• The smaller the angle $\theta$ between two vectors is, the larger $\cos \theta$ is.

• The maximum value of $\cos \theta$ is 1, achieved when $\theta = 0$.

• Key idea: The more similar two vectors are, the larger $\cos \theta$ is!

Cosine similarity

• To measure the similarity between two documents, we can compute the cosine similarity of their vector representations:

$$\text{cosine similarity}(\vec u, \vec v) = \cos \theta = \boxed{\frac{\vec{u} \cdot \vec{v}}{|\vec{u}| | \vec{v}|}}$$

• If all elements in $\vec{u}$ and $\vec{v}$ are non-negative, then $\cos \theta$ ranges from 0 to 1.

• Key idea: The more similar two vectors are, the larger $\cos \theta$ is!

• Given a collection of documents, to find the most similiar pair, we can:
  1. Find the vector representation of each document.
  2. Find the cosine similarity of each pair of vectors.
  3. Return the documents whose vectors had the largest cosine similarity.

Activity

Consider the matrix of word counts we found earlier, using the bag of words model:

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

1. Which two documents have the highest dot product?
2. Which two documents have the highest cosine similarity?

Normalizing

• Why can't we just use the dot product – that is, why must we divide by $|\vec{u}| | \vec{v}|$ when computing cosine similarity?

$$\text{cosine similarity}(\vec u, \vec v) = \cos \theta = \boxed{\frac{\vec{u} \cdot \vec{v}}{|\vec{u}| | \vec{v}|}}$$

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• Consider the following two pairs of documents:

Pair	Dot Product	Cosine Similarity
big big big big data class and data big data science	6	0.577
science big data and data big data science	4	0.943

• "big big big big data class" has a large dot product with "data big data science" just because the former has the term "big" four times. But intuitively, "data big data science" and "science big data" should be much more similar, since they have almost the exact same terms.

• So, make sure to compute the cosine similarity – don't just use the dot product!
  If you don't normalize by the lengths of the vectors, documents with more terms will have artificially high similarities with other documents.

Reference Slide

Cosine distance

• Sometimes, you will see the cosine distance being used. It is the complement of cosine similarity:

$$\text{dist}(\vec{u}, \vec{v}) = 1 - \text{cosine similarity}(\vec u, \vec v) = 1 - \cos \theta$$

• If $\text{dist}(\vec{u}, \vec{v})$ is small, the two vector representations are similar.

Issues with the bag of words model

• Recall, the bag of words model encodes a document as a vector containing word frequencies.

• It doesn't consider the order of the terms.

"big data science" and "data science big" have the same vector representation, but mean different things.

• It doesn't consider the meaning of terms.
  "I really really hate data" and "I really really love data" have nearly identical vector representations, but very different meanings.

• It treats all words as being equally important. This is the issue we'll address today.
  In "I am a student" and "I am a teacher", it's clear to us humans that the most important terms are "student" and "teacher", respectively. But in the bag of words model, "student" and "I" appear the same number of times in the first document.

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

What questions do you have?

TF-IDF

---

What makes a word important?

• Issue: The bag of words model doesn't know which terms are "important" in a document.

• Consider the following document:

"my brother has a friend named billy who has an uncle named billy"

• "has" and "billy" both appear the same number of times in the document above. But "has" is an extremely common term overall, while "billy" isn't.

• Observation: If a term is important in a document, it will appear frequently in that document but not frequently in other documents.
  Let's try and find a way of giving scores to terms that keeps this in mind. If we can do this, then the terms with the highest scores can be used to summarize the document!

Term frequency

• The term frequency of a term $t$ in a document $d$, denoted $\text{tf}(t, d)$, is the proportion of words in document $d$ that are equal to $t$.

$$\text{tf}(t, d) = \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}$$

• Example: What is the term frequency of "billy" in the following document?

"my brother has a friend named billy who has an uncle named billy"

• Answer: $\frac{2}{13}$.

• Intuition: Terms that occur often within a document are important to the document's meaning.

$$\text{tf}(t, d) \text{ large} \implies t \text{ occurs often in $d$} \\ \text{tf}(t, d) \text{ small} \implies t \text{ occurs rarely in $d$}$$

• Issue: "has" also has a TF of $\frac{2}{13}$, but it seems less important than "billy".

Inverse document frequency

• The inverse document frequency of a term $t$ in a set of documents $d_1, d_2, ...$ is:

$$\text{idf}(t) = \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right)$$

• Example: What is the inverse document frequency of "billy" in the following three documents?
  • "my brother has a friend named billy who has an uncle named billy"
  • "my favorite artist is named jilly boel"
  • "why does he talk about someone named billy so often"

• Answer: $\log \left(\frac{3}{2}\right) \approx 0.4055$.
  Here, we used the natural logarithm. It doesn't matter which log base we use, as long as we keep it consistent throughout all of our calculations.

• Intuition: If a word appears in every document (like "the" or "has"), it is probably not a good summary of any one document.

• Think of $\text{idf}(t)$ as the "rarity factor" of $t$ across documents – the larger $\text{idf}(t)$ is, the more rare $t$ is.

$$\text{idf}(t) \text{ large} \implies t \text{ rare across all documents} \\ \text{idf}(t) \text{ small} \implies t \text{ common across all documents}$$

Intuition

• Goal: Measure how important term $t$ is to document $d$.
  Equivalent goal: Find the terms that best summarize $d$.

$$\text{tf}(t, d) = \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}$$$$\text{idf}(t) = \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right)$$

• If $\text{tf}(t, d)$ is small, then $t$ doesn't occur very often in $d$, so $t$ can't be very important to $d$.

• If $\text{idf}(t)$ is small, then $t$ occurs often amongst all documents, and so it can't be very important to $d$ specifically.

• If $\text{tf}(t, d)$ and $\text{idf}(t)$ are both large, then $t$ occurs often in $d$ but rarely overall. This makes $t$ important to $d$, i.e. a good "summary" of $d$.

Term frequency-inverse document frequency

• The term frequency-inverse document frequency (TF-IDF) of term $t$ in document $d$ is the product:

$$ \begin{align*}\text{tfidf}(t, d) &= \text{tf}(t, d) \cdot \text{idf}(t) \\\ &= \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right) \end{align*} $$

• If $\text{tfidf}(t, d)$ is large, then $t$ is important to $d$, because $t$ occurs often in $d$ but rarely across all documents.
  This means $t$ is a good summary of $d$!

• Note: TF-IDF is a heuristic method – there's no "proof" that it performs well.

• To know if $\text{tfidf}(t, d)$ is large for one particular term $t$, we need to compare it to $\text{tfidf}(t_i, d)$, for several different terms $t_i$.

Computing TF-IDF

• Question: What is the TF-IDF of "science" in "data big data science"?

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• Answer:

$$\begin{align*}\text{tfidf}(t, d) &= \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right) \\ &= \frac{1}{4} \cdot \log\left( \frac{3}{2} \right)\end{align*} $$

• Question: Is this big or small? Is "science" the best summary of "data big data science"?

TF-IDF of all terms in all documents

• On its own, the TF-IDF of one term in one document doesn't really tell us anything. We must compare it to TF-IDFs of other terms in that same document.

• Let's start with a DataFrame version of our bag of words matrix. It already contains the numerators for term frequency, i.e. $\text{tf}(t, d) = \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}$.

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

bow = pd.DataFrame([[4, 1, 1, 0], [1, 2, 0, 1], [1, 1, 0, 1]],
                   index=['big big big big data class', 'data big data science', 'science big data'],
                   columns=['big', 'data', 'class', 'science'])
bow

	big	data	class	science
big big big big data class	4	1	1	0
data big data science	1	2	0	1
science big data	1	1	0	1

• The following cell converts the bag of words matrix above to a matrix with TF-IDF scores. See the comments for details.

# To convert the term counts to term frequencies, we'll divide by the sum of each row.
# Each row corresponds to the terms in one document; the sum of a row is the total number of terms in the document, 
# which is the denominator in the formula for term frequency, (# of occurrences of t in d) / (total # of terms in d).
tfs = bow.apply(lambda s: s / s.sum(), axis=1)
# Next, we need to find the inverse document frequency of each term, t, 
# where idf(t) = log(total # of documents / # of documents in which t appears).
def idf(term):
    term_column = tfs[term]
    return np.log(term_column.shape[0] / (term_column > 0).sum())
all_idfs = [idf(c) for c in tfs.columns]
all_idfs = pd.Series(all_idfs, index=tfs.columns)
# Finally, let's multiply `tfs`, the DataFrame with the term frequencies of each term in each document, 
# by `all_idfs`, the Series of inverse document frequencies of each term.
tfidfs = tfs * all_idfs
tfidfs

	big	data	class	science
big big big big data class	0.0	0.0	0.18	0.00
data big data science	0.0	0.0	0.00	0.10
science big data	0.0	0.0	0.00	0.14

Interpreting TF-IDFs

tfidfs

	big	data	class	science
big big big big data class	0.0	0.0	0.18	0.00
data big data science	0.0	0.0	0.00	0.10
science big data	0.0	0.0	0.00	0.14

• The TF-IDF of 'class' in the first sentence is $\approx 0.18$.

• The TF-IDF of 'data' in the second sentence is 0.

• Note that there are two ways that $\text{tfidf}(t, d) = \text{tf}(t, d) \cdot \text{idf}(t)$ can be 0:
  • If $t$ appears in every document, because then $\text{idf}(t) = \log (\frac{\text{# documents}}{\text{# documents}}) = \log(1) = 0$.
  • If $t$ does not appear in document $d$, because then $\text{tf}(t, d) = \frac{0}{\text{len}(d)} = 0$.

• The term that best summarizes a document is the term with the highest TF-IDF for that document:

tfidfs.idxmax(axis=1) 

big big big big data class      class
data big data science         science
science big data              science
dtype: object

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

What questions do you have?

Activity

Work on Problem 13 in the "Regular Expressions and Text Features" worksheet.

Example: State of the Union addresses 🎤

---

Overview

• Now that we have a robust technique for assigning scores to terms – that is, TF-IDF – we can use it to find the most important terms in each State of the Union address.

speeches

	text
George Washington: January 8, 1790	fellow citizens of the senate and house of re...
George Washington: December 8, 1790	fellow citizens of the senate and house of re...
George Washington: October 25, 1791	fellow citizens of the senate and house of re...
...	...
Joseph R. Biden Jr.: February 7, 2023	mr speaker madam vice president our firs...
Joseph R. Biden Jr.: March 7, 2024	good evening mr speaker madam vice presi...
Donald J. Trump: March 4, 2025	the president thank you thank you very much...

235 rows × 1 columns

• To recap, we'll need to compute:

        for each term t:
            for each speech d:
                compute tfidf(t, d)

• We've provided the implementation details in reference slides so you can refer to them in Homework 6.

Reference Slide

Finding all unique terms

• First, we need to find the unique terms used across all SOTU speeches.
  These words will form the columns of our TF-IDF matrix.

all_unique_terms = speeches['text'].str.split().explode().value_counts()
all_unique_terms

text
the           147744
of             94765
and            61192
               ...  
pathos             1
desirables         1
skylines           1
Name: count, Length: 24528, dtype: int64

• Since there are over 20,000 unique terms, our future calculations will otherwise take too much time to run. Let's take the 500 most frequent, across all speeches, for speed.

unique_terms = all_unique_terms.iloc[:500].index
unique_terms

Index(['the', 'of', 'and', 'to', 'in', 'a', 'that', 'for', 'be', 'our',
       ...
       'abroad', 'demand', 'call', 'old', 'think', 'throughout', 'increasing',
       'desire', 'submitted', 'building'],
      dtype='object', name='text', length=500)

Reference Slide

Finding term frequencies

• Next, let's find the bag of words matrix, i.e. a matrix that tells us the number of occurrences of each term in each document.

• What's the difference between the following two expressions?

speeches['text'].str.count('the')

George Washington: January 8, 1790       120
George Washington: December 8, 1790      160
George Washington: October 25, 1791      302
                                        ... 
Joseph R. Biden Jr.: February 7, 2023    507
Joseph R. Biden Jr.: March 7, 2024       399
Donald J. Trump: March 4, 2025           673
Name: text, Length: 235, dtype: int64

# Remember, the \b special character matches **word boundaries**!
# This makes sure that we don't count instances of "the" that are part of other words,
# like "thesaurus".
speeches['text'].str.count(r'\bthe\b')

George Washington: January 8, 1790        97
George Washington: December 8, 1790      122
George Washington: October 25, 1791      242
                                        ... 
Joseph R. Biden Jr.: February 7, 2023    338
Joseph R. Biden Jr.: March 7, 2024       293
Donald J. Trump: March 4, 2025           411
Name: text, Length: 235, dtype: int64

• Let's repeat the above calculation for every unique term. This code will take a while to run, so we'll use the tdqm package to track its progress.
  Install with mamba install tqdm if needed.

from tqdm.notebook import tqdm
counts_dict = {}
for term in tqdm(unique_terms):
    counts_dict[term] = speeches['text'].str.count(fr'\b{term}\b')        
counts = pd.DataFrame(counts_dict, index=speeches.index)
counts

	the	of	and	to	...	increasing	desire	submitted	building
George Washington: January 8, 1790	97	69	41	56	...	1	0	0	0
George Washington: December 8, 1790	122	89	45	49	...	0	0	1	0
George Washington: October 25, 1791	242	159	73	88	...	1	0	1	0
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: February 7, 2023	338	166	232	261	...	2	0	0	6
Joseph R. Biden Jr.: March 7, 2024	293	132	234	216	...	1	0	0	5
Donald J. Trump: March 4, 2025	411	260	418	296	...	0	0	0	6

235 rows × 500 columns

• The above DataFrame does not contain term frequencies. To convert the values above to term frequencies, we need to normalize by the sum of each row.

tfs = counts.apply(lambda s: s / s.sum(), axis=1)
tfs

	the	of	and	to	...	increasing	desire	submitted	building
George Washington: January 8, 1790	0.12	0.09	0.05	0.07	...	1.25e-03	0.0	0.00e+00	0.00e+00
George Washington: December 8, 1790	0.12	0.09	0.04	0.05	...	0.00e+00	0.0	9.86e-04	0.00e+00
George Washington: October 25, 1791	0.15	0.10	0.04	0.05	...	6.02e-04	0.0	6.02e-04	0.00e+00
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: February 7, 2023	0.07	0.04	0.05	0.06	...	4.23e-04	0.0	0.00e+00	1.27e-03
Joseph R. Biden Jr.: March 7, 2024	0.07	0.03	0.06	0.05	...	2.42e-04	0.0	0.00e+00	1.21e-03
Donald J. Trump: March 4, 2025	0.06	0.04	0.06	0.04	...	0.00e+00	0.0	0.00e+00	8.76e-04

235 rows × 500 columns

Reference Slide

Finding TF-IDFs

• Finally, we'll need to find the inverse document frequencies (IDF) of each term.

• Using apply, we can find the IDFs of each term and multiply them by the term frequencies in one step.

$$\begin{align*}\text{tfidf}(t, d) &= \underbrace{\frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}}}_{\text{we already computed these}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right)\end{align*} $$

tfidfs = tfs.apply(lambda s: s * np.log(s.shape[0] / (s > 0).sum()))
tfidfs

	the	of	and	to	...	increasing	desire	submitted	building
George Washington: January 8, 1790	0.0	0.0	0.0	0.0	...	5.20e-04	0.0	0.00e+00	0.00e+00
George Washington: December 8, 1790	0.0	0.0	0.0	0.0	...	0.00e+00	0.0	6.15e-04	0.00e+00
George Washington: October 25, 1791	0.0	0.0	0.0	0.0	...	2.51e-04	0.0	3.75e-04	0.00e+00
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: February 7, 2023	0.0	0.0	0.0	0.0	...	1.76e-04	0.0	0.00e+00	6.04e-04
Joseph R. Biden Jr.: March 7, 2024	0.0	0.0	0.0	0.0	...	1.01e-04	0.0	0.00e+00	5.76e-04
Donald J. Trump: March 4, 2025	0.0	0.0	0.0	0.0	...	0.00e+00	0.0	0.00e+00	4.17e-04

235 rows × 500 columns

• Why are the TF-IDFs of many common words 0?

Summarizing speeches

• The DataFrame tfidfs now has the TF-IDF of every term in every speech.
  Why are the TF-IDFs of many common terms 0?

tfidfs

	the	of	and	to	...	increasing	desire	submitted	building
George Washington: January 8, 1790	0.0	0.0	0.0	0.0	...	5.20e-04	0.0	0.00e+00	0.00e+00
George Washington: December 8, 1790	0.0	0.0	0.0	0.0	...	0.00e+00	0.0	6.15e-04	0.00e+00
George Washington: October 25, 1791	0.0	0.0	0.0	0.0	...	2.51e-04	0.0	3.75e-04	0.00e+00
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: February 7, 2023	0.0	0.0	0.0	0.0	...	1.76e-04	0.0	0.00e+00	6.04e-04
Joseph R. Biden Jr.: March 7, 2024	0.0	0.0	0.0	0.0	...	1.01e-04	0.0	0.00e+00	5.76e-04
Donald J. Trump: March 4, 2025	0.0	0.0	0.0	0.0	...	0.00e+00	0.0	0.00e+00	4.17e-04

235 rows × 500 columns

• By using idxmax, we can find the term with the highest TF-IDF in each speech.

summaries = tfidfs.idxmax(axis=1) 
summaries

George Washington: January 8, 1790            ought
George Washington: December 8, 1790      convention
George Washington: October 25, 1791       provision
                                            ...    
Joseph R. Biden Jr.: February 7, 2023       tonight
Joseph R. Biden Jr.: March 7, 2024          tonight
Donald J. Trump: March 4, 2025              tonight
Length: 235, dtype: object

• What if we want to see the 5 terms with the highest TF-IDFs, for each speech?

def five_largest(row):
    return ', '.join(row.index[row.argsort()][-5:])

keywords = tfidfs.apply(five_largest, axis=1).to_frame().rename(columns={0: 'most important terms'})
keywords

	most important terms
George Washington: January 8, 1790	your, opinion, proper, regard, ought
George Washington: December 8, 1790	welfare, case, established, commerce, convention
George Washington: October 25, 1791	community, upon, lands, proper, provision
...	...
Joseph R. Biden Jr.: February 7, 2023	down, percent, let, jobs, tonight
Joseph R. Biden Jr.: March 7, 2024	jobs, down, get, americans, tonight
Donald J. Trump: March 4, 2025	you, want, get, million, tonight

235 rows × 1 columns

• Uncomment the cell below to see every single row of keywords.
  Cool!

display_df(keywords, rows=235)

	most important terms
George Washington: January 8, 1790	your, opinion, proper, regard, ought
George Washington: December 8, 1790	welfare, case, established, commerce, convention
George Washington: October 25, 1791	community, upon, lands, proper, provision
George Washington: November 6, 1792	subject, upon, information, proper, provision
George Washington: December 3, 1793	territory, vessels, executive, shall, ought
George Washington: November 19, 1794	laws, army, let, ought, constitution
George Washington: December 8, 1795	representatives, information, prevent, provisi...
George Washington: December 7, 1796	establishment, republic, treaty, britain, ought
John Adams: November 22, 1797	spain, british, claims, treaty, vessels
John Adams: December 8, 1798	st, minister, treaty, spain, commerce
John Adams: December 3, 1799	civil, period, british, minister, treaty
John Adams: November 11, 1800	experience, protection, navy, commerce, ought
Thomas Jefferson: December 8, 1801	revenue, consideration, shall, vessels, subject
Thomas Jefferson: December 15, 1802	shall, debt, naval, duties, vessels
Thomas Jefferson: October 17, 1803	debt, vessels, sum, millions, friendly
Thomas Jefferson: November 8, 1804	received, having, convention, due, friendly
Thomas Jefferson: December 3, 1805	families, convention, sum, millions, vessels
Thomas Jefferson: December 2, 1806	due, consideration, millions, shall, spain
Thomas Jefferson: October 27, 1807	whether, army, british, vessels, shall
Thomas Jefferson: November 8, 1808	shall, british, millions, commerce, her
James Madison: November 29, 1809	cases, having, due, british, minister
James Madison: December 5, 1810	provisions, view, minister, commerce, british
James Madison: November 5, 1811	britain, provisions, commerce, minister, british
James Madison: November 4, 1812	nor, subject, provisions, britain, british
James Madison: December 7, 1813	number, having, naval, britain, british
James Madison: September 20, 1814	naval, vessels, britain, his, british
James Madison: December 5, 1815	debt, treasury, millions, establishment, sum
James Madison: December 3, 1816	annual, constitution, sum, treasury, british
James Monroe: December 12, 1817	improvement, territory, indian, millions, lands
James Monroe: November 16, 1818	revenue, minister, territory, her, spain
James Monroe: December 7, 1819	parties, friendly, minister, treaty, spain
James Monroe: November 14, 1820	amount, minister, extent, vessels, spain
James Monroe: December 3, 1821	powers, duties, revenue, spain, vessels
James Monroe: December 3, 1822	duties, proper, vessels, spain, convention
James Monroe: December 2, 1823	powers, th, department, minister, spain
James Monroe: December 7, 1824	commerce, spain, governments, convention, parties
John Quincy Adams: December 6, 1825	establishment, commerce, condition, upon, impr...
John Quincy Adams: December 5, 1826	commercial, upon, vessels, british, duties
John Quincy Adams: December 4, 1827	lands, british, receipts, upon, th
John Quincy Adams: December 2, 1828	duties, revenue, upon, commercial, britain
Andrew Jackson: December 8, 1829	attention, subject, her, upon, duties
Andrew Jackson: December 6, 1830	general, subject, vessels, character, upon
Andrew Jackson: December 6, 1831	indian, commerce, claims, treaty, minister
Andrew Jackson: December 4, 1832	general, subject, duties, lands, commerce
Andrew Jackson: December 3, 1833	treasury, convention, minister, spain, duties
Andrew Jackson: December 1, 1834	subject, minister, treaty, claims, upon
Andrew Jackson: December 7, 1835	treaty, upon, claims, subject, minister
Andrew Jackson: December 5, 1836	upon, treasury, duties, revenue, banks
Martin van Buren: December 5, 1837	price, subject, upon, banks, lands
Martin van Buren: December 3, 1838	subject, upon, indian, banks, court
Martin van Buren: December 2, 1839	treasury, duties, extent, institutions, banks
Martin van Buren: December 5, 1840	general, revenue, having, upon, extent
John Tyler: December 7, 1841	consideration, britain, amount, duties, treasury
John Tyler: December 6, 1842	claims, minister, thus, amount, treasury
John Tyler: December 6, 1843	subject, british, her, minister, mexico
John Tyler: December 3, 1844	minister, upon, treaty, her, mexico
James Polk: December 2, 1845	british, convention, territory, duties, mexico
James Polk: December 8, 1846	army, territory, minister, her, mexico
James Polk: December 7, 1847	amount, treaty, her, army, mexico
James Polk: December 5, 1848	tariff, upon, bill, constitution, mexico
Zachary Taylor: December 4, 1849	territory, treaty, recommend, minister, mexico
Millard Fillmore: December 2, 1850	recommend, claims, upon, mexico, duties
Millard Fillmore: December 2, 1851	department, annual, fiscal, subject, mexico
Millard Fillmore: December 6, 1852	duties, navy, mexico, subject, her
Franklin Pierce: December 5, 1853	commercial, regard, construction, upon, subject
Franklin Pierce: December 4, 1854	character, duties, naval, minister, property
Franklin Pierce: December 31, 1855	constitution, british, territory, convention, ...
Franklin Pierce: December 2, 1856	constitution, property, condition, thus, terri...
James Buchanan: December 8, 1857	treaty, territory, constitution, convention, b...
James Buchanan: December 6, 1858	shall, mexico, minister, constitution, territory
James Buchanan: December 19, 1859	republic, th, fiscal, mexico, june
James Buchanan: December 3, 1860	minister, duties, claims, convention, constitu...
Abraham Lincoln: December 3, 1861	army, claims, labor, capital, court
Abraham Lincoln: December 1, 1862	upon, population, shall, per, sum
Abraham Lincoln: December 8, 1863	upon, receipts, subject, navy, naval
Abraham Lincoln: December 6, 1864	condition, secretary, treasury, naval, navy
Andrew Johnson: December 4, 1865	form, commerce, powers, general, constitution
Andrew Johnson: December 3, 1866	thus, june, constitution, mexico, condition
Andrew Johnson: December 3, 1867	june, value, department, upon, constitution
Andrew Johnson: December 9, 1868	millions, amount, expenditures, june, per
Ulysses S. Grant: December 6, 1869	subject, upon, receipts, per, spain
Ulysses S. Grant: December 5, 1870	her, convention, vessels, spain, british
Ulysses S. Grant: December 4, 1871	navy, powers, desire, treaty, recommend
Ulysses S. Grant: December 2, 1872	territory, line, her, britain, treaty
Ulysses S. Grant: December 1, 1873	consideration, subject, amount, banks, claims
Ulysses S. Grant: December 7, 1874	duties, upon, attention, claims, convention
Ulysses S. Grant: December 7, 1875	parties, territory, court, spain, claims
Ulysses S. Grant: December 5, 1876	court, subject, per, commission, claims
Rutherford B. Hayes: December 3, 1877	upon, sum, fiscal, commercial, value
Rutherford B. Hayes: December 2, 1878	per, fiscal, june, secretary, indian
Rutherford B. Hayes: December 1, 1879	subject, territory, june, commission, indian
Rutherford B. Hayes: December 6, 1880	office, subject, relations, attention, commercial
Chester A. Arthur: December 6, 1881	spain, international, british, relations, frie...
Chester A. Arthur: December 4, 1882	territory, mexico, establishment, internationa...
Chester A. Arthur: December 4, 1883	claims, convention, mexico, commission, treaty
Chester A. Arthur: December 1, 1884	treaty, territory, commercial, secretary, vessels
Grover Cleveland: December 8, 1885	duties, vessels, treaty, condition, upon
Grover Cleveland: December 6, 1886	mexico, claims, subject, convention, fiscal
Grover Cleveland: December 6, 1887	condition, sum, thus, price, tariff
Grover Cleveland: December 3, 1888	treaty, upon, secretary, per, june
Benjamin Harrison: December 3, 1889	general, commission, indian, upon, lands
Benjamin Harrison: December 1, 1890	receipts, subject, upon, per, tariff
Benjamin Harrison: December 9, 1891	court, tariff, indian, upon, per
Benjamin Harrison: December 6, 1892	tariff, secretary, upon, value, per
William McKinley: December 6, 1897	conditions, international, upon, territory, spain
William McKinley: December 5, 1898	commission, navy, naval, june, spain
William McKinley: December 5, 1899	treaty, officers, commission, international, c...
William McKinley: December 3, 1900	settlement, civil, shall, convention, commission
Theodore Roosevelt: December 3, 1901	army, commercial, conditions, navy, man
Theodore Roosevelt: December 2, 1902	man, upon, navy, conditions, tariff
Theodore Roosevelt: December 7, 1903	june, lands, territory, property, treaty
Theodore Roosevelt: December 6, 1904	cases, conditions, indian, labor, man
Theodore Roosevelt: December 5, 1905	upon, conditions, commission, cannot, man
Theodore Roosevelt: December 3, 1906	upon, navy, tax, court, man
Theodore Roosevelt: December 3, 1907	conditions, navy, upon, army, man
Theodore Roosevelt: December 8, 1908	man, officers, labor, control, banks
William H. Taft: December 7, 1909	convention, banks, court, department, tariff
William H. Taft: December 6, 1910	department, court, commercial, international, ...
William H. Taft: December 5, 1911	commission, department, per, tariff, court
William H. Taft: December 3, 1912	republic, upon, army, per, department
Woodrow Wilson: December 2, 1913	how, shall, upon, mexico, ought
Woodrow Wilson: December 8, 1914	shall, convention, ought, matter, upon
Woodrow Wilson: December 7, 1915	her, millions, navy, economic, cannot
Woodrow Wilson: December 5, 1916	commerce, upon, shall, bill, commission
Woodrow Wilson: December 4, 1917	desire, her, know, settlement, shall
Woodrow Wilson: December 2, 1918	go, shall, men, back, upon
Woodrow Wilson: December 2, 1919	america, her, budget, labor, conditions
Woodrow Wilson: December 7, 1920	expenditures, receipts, budget, treasury, upon
Warren Harding: December 6, 1921	ought, capital, problems, conditions, tariff
Warren Harding: December 8, 1922	responsibility, republic, problems, ought, per
Calvin Coolidge: December 6, 1923	conditions, production, commission, ought, court
Calvin Coolidge: December 3, 1924	international, navy, desire, economic, court
Calvin Coolidge: December 8, 1925	upon, budget, economic, ought, court
Calvin Coolidge: December 7, 1926	banks, federal, reduction, tariff, ought
Calvin Coolidge: December 6, 1927	construction, banks, per, program, property
Calvin Coolidge: December 4, 1928	federal, production, department, program, per
Herbert Hoover: December 3, 1929	federal, commission, construction, tariff, per
Herbert Hoover: December 2, 1930	about, budget, economic, per, construction
Herbert Hoover: December 8, 1931	upon, construction, federal, economic, banks
Herbert Hoover: December 6, 1932	health, june, value, economic, banks
Franklin D. Roosevelt: January 3, 1934	labor, permanent, problems, cannot, banks
Franklin D. Roosevelt: January 4, 1935	private, work, local, program, cannot
Franklin D. Roosevelt: January 3, 1936	world, shall, let, say, today
Franklin D. Roosevelt: January 6, 1937	powers, convention, needs, help, problems
Franklin D. Roosevelt: January 3, 1938	budget, business, economic, today, income
Franklin D. Roosevelt: January 4, 1939	labor, cannot, capital, income, billion
Franklin D. Roosevelt: January 3, 1940	world, domestic, cannot, economic, today
Franklin D. Roosevelt: January 6, 1941	freedom, problems, cannot, program, today
Franklin D. Roosevelt: January 6, 1942	today, shall, know, forces, production
Franklin D. Roosevelt: January 7, 1943	get, pacific, cannot, americans, production
Franklin D. Roosevelt: January 11, 1944	individual, total, know, economic, cannot
Franklin D. Roosevelt: January 6, 1945	cannot, production, forces, army, jobs
Harry S. Truman: January 21, 1946	fiscal, program, billion, million, dollars
Harry S. Truman: January 6, 1947	commission, budget, economic, labor, program
Harry S. Truman: January 7, 1948	tax, billion, today, program, economic
Harry S. Truman: January 5, 1949	economic, price, program, cannot, production
Harry S. Truman: January 4, 1950	income, today, program, programs, economic
Harry S. Truman: January 8, 1951	help, program, production, strength, economic
Harry S. Truman: January 9, 1952	defense, working, program, help, production
Harry S. Truman: January 7, 1953	republic, free, cannot, world, economic
Dwight D. Eisenhower: February 2, 1953	federal, labor, budget, economic, programs
Dwight D. Eisenhower: January 7, 1954	federal, programs, economic, budget, program
Dwight D. Eisenhower: January 6, 1955	problems, federal, economic, programs, program
Dwight D. Eisenhower: January 5, 1956	billion, federal, problems, economic, program
Dwight D. Eisenhower: January 10, 1957	programs, human, program, economic, today
Dwight D. Eisenhower: January 9, 1958	effort, today, strength, programs, economic
Dwight D. Eisenhower: January 9, 1959	growth, help, billion, programs, economic
Dwight D. Eisenhower: January 7, 1960	cannot, freedom, economic, today, help
Dwight D. Eisenhower: January 12, 1961	million, percent, billion, program, programs
John F. Kennedy: January 30, 1961	development, programs, problems, economic, pro...
John F. Kennedy: January 11, 1962	billion, help, program, jobs, cannot
John F. Kennedy: January 14, 1963	today, cannot, tax, percent, billion
Lyndon B. Johnson: January 8, 1964	help, billion, americans, budget, million
Lyndon B. Johnson: January 4, 1965	americans, man, programs, tonight, help
Lyndon B. Johnson: January 12, 1966	program, percent, help, billion, tonight
Lyndon B. Johnson: January 10, 1967	programs, americans, billion, tonight, percent
Lyndon B. Johnson: January 17, 1968	programs, million, budget, tonight, billion
Lyndon B. Johnson: January 14, 1969	program, billion, budget, think, tonight
Richard Nixon: January 22, 1970	billion, percent, america, today, programs
Richard Nixon: January 22, 1971	america, americans, tonight, budget, let
Richard Nixon: January 20, 1972	program, america, programs, help, today
Richard Nixon: February 2, 1973	economic, help, americans, working, programs
Richard Nixon: January 30, 1974	americans, america, today, energy, tonight
Gerald R. Ford: January 15, 1975	program, percent, billion, programs, energy
Gerald R. Ford: January 19, 1976	federal, americans, budget, jobs, programs
Gerald R. Ford: January 12, 1977	programs, today, percent, jobs, energy
Jimmy Carter: January 19, 1978	tax, cannot, economic, tonight, jobs
Jimmy Carter: January 25, 1979	help, cannot, budget, tonight, americans
Jimmy Carter: January 21, 1980	economic, help, energy, tonight, america
Jimmy Carter: January 16, 1981	administration, economic, energy, program, pro...
Ronald Reagan: January 26, 1982	jobs, help, program, billion, programs
Ronald Reagan: January 25, 1983	problems, programs, americans, economic, percent
Ronald Reagan: January 25, 1984	percent, budget, help, americans, tonight
Ronald Reagan: February 6, 1985	growth, help, tax, jobs, tonight
Ronald Reagan: February 4, 1986	families, cannot, america, budget, tonight
Ronald Reagan: January 27, 1987	percent, america, budget, tonight, let
Ronald Reagan: January 25, 1988	americans, america, budget, let, tonight
George H.W. Bush: February 9, 1989	ask, america, let, budget, tonight
George H.W. Bush: January 31, 1990	percent, america, budget, today, tonight
George H.W. Bush: January 29, 1991	jobs, budget, americans, know, tonight
George H.W. Bush: January 28, 1992	jobs, know, get, tonight, help
William J. Clinton: February 17, 1993	tax, budget, percent, tonight, jobs
William J. Clinton: January 25, 1994	care, americans, health, get, jobs
William J. Clinton: January 24, 1995	jobs, americans, let, get, tonight
William J. Clinton: January 23, 1996	tonight, families, working, americans, children
William J. Clinton: February 4, 1997	america, children, budget, americans, tonight
William J. Clinton: January 27, 1998	ask, americans, children, help, tonight
William J. Clinton: January 19, 1999	today, budget, help, americans, tonight
William J. Clinton: January 27, 2000	families, help, americans, children, tonight
George W. Bush: February 27, 2001	help, tax, percent, tonight, budget
George W. Bush: September 20, 2001	freedom, america, ask, americans, tonight
George W. Bush: January 29, 2002	americans, budget, tonight, america, jobs
George W. Bush: January 28, 2003	america, help, million, americans, tonight
George W. Bush: January 20, 2004	children, america, americans, help, tonight
George W. Bush: February 2, 2005	freedom, tonight, help, social, americans
George W. Bush: January 31, 2006	reform, jobs, americans, america, tonight
George W. Bush: January 23, 2007	america, health, americans, tonight, help
George W. Bush: January 29, 2008	ask, americans, america, tonight, help
Barack Obama: February 24, 2009	banks, know, budget, jobs, tonight
Barack Obama: January 27, 2010	families, get, tonight, americans, jobs
Barack Obama: January 25, 2011	percent, americans, get, tonight, jobs
Barack Obama: January 24, 2012	energy, americans, tonight, get, jobs
Barack Obama: February 12, 2013	let, families, get, tonight, jobs
Barack Obama: January 28, 2014	get, americans, tonight, help, jobs
Barack Obama: January 20, 2015	let, families, americans, tonight, jobs
Barack Obama: January 12, 2016	tonight, america, jobs, americans, get
Donald J. Trump: February 27, 2017	down, america, jobs, americans, tonight
Donald J. Trump: January 30, 2018	tax, america, get, americans, tonight
Donald J. Trump: February 5, 2019	get, america, jobs, americans, tonight
Donald J. Trump: February 4, 2020	america, jobs, americans, percent, tonight
Joseph R. Biden Jr.: April 28, 2021	america, get, americans, percent, jobs
Joseph R. Biden Jr.: March 1, 2022	percent, jobs, get, americans, tonight
Joseph R. Biden Jr.: February 7, 2023	down, percent, let, jobs, tonight
Joseph R. Biden Jr.: March 7, 2024	jobs, down, get, americans, tonight
Donald J. Trump: March 4, 2025	you, want, get, million, tonight

Cosine similarity, revisited

• Each row of tfidfs contains a vector representation of a speech. This means that we can compute the cosine similarities between any two speeches!
  The only difference now is that we used TF-IDF to find $\vec u$ and $\vec v$, rather than the bag of words model.

$$\text{cosine similarity}(\vec u, \vec v) = \frac{\vec{u} \cdot \vec{v}}{|\vec{u}| | \vec{v}|}$$

tfidfs

	the	of	and	to	...	increasing	desire	submitted	building
George Washington: January 8, 1790	0.0	0.0	0.0	0.0	...	5.20e-04	0.0	0.00e+00	0.00e+00
George Washington: December 8, 1790	0.0	0.0	0.0	0.0	...	0.00e+00	0.0	6.15e-04	0.00e+00
George Washington: October 25, 1791	0.0	0.0	0.0	0.0	...	2.51e-04	0.0	3.75e-04	0.00e+00
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: February 7, 2023	0.0	0.0	0.0	0.0	...	1.76e-04	0.0	0.00e+00	6.04e-04
Joseph R. Biden Jr.: March 7, 2024	0.0	0.0	0.0	0.0	...	1.01e-04	0.0	0.00e+00	5.76e-04
Donald J. Trump: March 4, 2025	0.0	0.0	0.0	0.0	...	0.00e+00	0.0	0.00e+00	4.17e-04

235 rows × 500 columns

def sim(speech_1, speech_2):
    v1 = tfidfs.loc[speech_1]
    v2 = tfidfs.loc[speech_2]
    return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))

sim('George Washington: January 8, 1790', 'George Washington: December 8, 1790')

0.4808392552136325

sim('George Washington: January 8, 1790', 'Donald J. Trump: March 4, 2025')

0.09111229184834736

• We can also find the most similar pair of speeches:

from itertools import combinations
sims_dict = {}
# For every pair of speeches, find the similarity and store it in
# the sims_dict dictionary.
for pair in combinations(tfidfs.index, 2):
    sims_dict[pair] = sim(pair[0], pair[1])
# Turn the sims_dict dictionary into a DataFrame.
sims = (
    pd.Series(sims_dict)
    .reset_index()
    .rename(columns={'level_0': 'speech 1', 'level_1': 'speech 2', 0: 'cosine similarity'})
    .sort_values('cosine similarity', ascending=False)
)
sims

	speech 1	speech 2	cosine similarity
11742	James Polk: December 8, 1846	James Polk: December 7, 1847	0.93
27391	Barack Obama: January 25, 2011	Barack Obama: February 12, 2013	0.93
27404	Barack Obama: January 24, 2012	Barack Obama: February 12, 2013	0.92
...	...	...	...
6744	James Monroe: December 7, 1819	Ronald Reagan: January 26, 1982	0.04
18290	Grover Cleveland: December 6, 1887	George W. Bush: September 20, 2001	0.04
6763	James Monroe: December 7, 1819	George W. Bush: February 27, 2001	0.03

27495 rows × 3 columns

• Or evevn the most similar pairs of speeches by different Presidents:

sims[sims['speech 1'].str.split(':').str[0] != sims['speech 2'].str.split(':').str[0]]

	speech 1	speech 2	cosine similarity
27412	Barack Obama: January 24, 2012	Joseph R. Biden Jr.: April 28, 2021	0.88
27470	Donald J. Trump: January 30, 2018	Joseph R. Biden Jr.: March 1, 2022	0.88
27465	Donald J. Trump: February 27, 2017	Joseph R. Biden Jr.: March 7, 2024	0.87
...	...	...	...
6744	James Monroe: December 7, 1819	Ronald Reagan: January 26, 1982	0.04
18290	Grover Cleveland: December 6, 1887	George W. Bush: September 20, 2001	0.04
6763	James Monroe: December 7, 1819	George W. Bush: February 27, 2001	0.03

26854 rows × 3 columns

Aside: What if we remove the $\log$ from $\text{idf}(t)$?

• Let's try it and see what happens.
  Below is another, quicker implementation of how we might find TF-IDFs.

tfidfs_nl_dict = {}
tf_denom = speeches['text'].str.split().str.len()
for word in tqdm(unique_terms):
    re_pat = fr' {word} ' # Imperfect pattern for speed.
    tf = speeches['text'].str.count(re_pat) / tf_denom
    idf_nl = len(speeches) / speeches['text'].str.contains(re_pat).sum()
    tfidfs_nl_dict[word] =  tf * idf_nl

tfidfs_nl = pd.DataFrame(tfidfs_nl_dict)
tfidfs_nl.head()

	the	of	and	to	...	increasing	desire	submitted	building
George Washington: January 8, 1790	0.09	0.06	0.04	0.05	...	1.39e-03	0.00e+00	0.00e+00	0.0
George Washington: December 8, 1790	0.09	0.06	0.03	0.03	...	0.00e+00	0.00e+00	1.33e-03	0.0
George Washington: October 25, 1791	0.11	0.07	0.03	0.04	...	6.58e-04	0.00e+00	8.09e-04	0.0
George Washington: November 6, 1792	0.09	0.07	0.03	0.04	...	0.00e+00	8.78e-04	0.00e+00	0.0
George Washington: December 3, 1793	0.09	0.07	0.02	0.04	...	0.00e+00	1.87e-03	0.00e+00	0.0

5 rows × 500 columns

keywords_nl = tfidfs_nl.apply(five_largest, axis=1)
keywords_nl

George Washington: January 8, 1790        a, and, to, of, the
George Washington: December 8, 1790      in, and, to, of, the
George Washington: October 25, 1791       a, and, to, of, the
                                                 ...         
Joseph R. Biden Jr.: February 7, 2023     a, of, and, to, the
Joseph R. Biden Jr.: March 7, 2024        a, of, to, and, the
Donald J. Trump: March 4, 2025            a, of, to, the, and
Length: 235, dtype: object

• What do you notice?

The role of $\log$ in $\text{idf}(t)$

$$ \begin{align*}\text{tfidf}(t, d) &= \text{tf}(t, d) \cdot \text{idf}(t) \\\ &= \frac{\text{# of occurrences of $t$ in $d$}}{\text{total # of terms in $d$}} \cdot \log \left(\frac{\text{total # of documents}}{\text{# of documents in which $t$ appears}} \right) \end{align*} $$

• Remember, for any positive input $x$, $\log(x)$ is (much) smaller than $x$.

• In $\text{idf}(t)$, the $\log$ "dampens" the impact of the ratio $\frac{\text{# documents}}{\text{# documents with $t$}}$. If a word is very common, the ratio will be close to 1. The log of the ratio will be close to 0.

(1000 / 999)

1.001001001001001

np.log(1000 / 999)

0.001000500333583622

• If a word is very common (e.g. "the"), and we didn't have the $\log$, we'd be multiplying the term frequency by a large factor.

• If a word is very rare, the ratio $\frac{\text{# documents}}{\text{# documents with $t$}}$ will be very large. However, for instance, a word being seen in 2 out of 50 documents is not very different than being seen in 2 out of 500 documents (it is very rare in both cases), and so $\text{idf}(t)$ should be similar in both cases.

(50 / 2)

25.0

(500 / 2)

250.0

np.log(50 / 2)

3.2188758248682006

np.log(500 / 2)

5.521460917862246

TF-IDF in practice

• In Homework 6, we will ask you to implement TF-IDF to further your own understanding.

• But, in practical projects – like the Final Project – you'd use an existing implementation of it, like TfIdfVectorizer in sklearn.
  See the documentation for more details.

from sklearn.feature_extraction.text import TfidfVectorizer

vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(speeches['text'])
tfidfs_sklearn = pd.DataFrame(X.toarray(), 
                              columns=vectorizer.get_feature_names_out(), 
                              index=speeches.index)

tfidfs_sklearn

	aaa	aaron	abandon	abandoned	...	zones	zoological	zooming	zuloaga
George Washington: January 8, 1790	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0
George Washington: December 8, 1790	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0
George Washington: October 25, 1791	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0
...	...	...	...	...	...	...	...	...	...
Joseph R. Biden Jr.: February 7, 2023	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0
Joseph R. Biden Jr.: March 7, 2024	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0
Donald J. Trump: March 4, 2025	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0

235 rows × 23998 columns

tfidfs_sklearn[tfidfs_sklearn['zuloaga'] != 0]

	aaa	aaron	abandon	abandoned	...	zones	zoological	zooming	zuloaga
James Buchanan: December 19, 1859	0.0	0.0	0.0	0.00e+00	...	0.0	0.0	0.0	1.34e-02
James Buchanan: December 3, 1860	0.0	0.0	0.0	1.30e-03	...	0.0	0.0	0.0	2.92e-03

2 rows × 23998 columns

What's next?

• The remainder of the semester will be more mathematical in nature.

• But, that mathematical understanding will enable us to perform more interesting analyses!

from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.decomposition import PCA
pipeline = make_pipeline(
    TfidfVectorizer(),
    PCA(n_components=2),
)
pipeline.fit(speeches['text'])
scores = pipeline.transform(speeches['text'])
fig = px.scatter(x=scores[:, 0], 
           y=scores[:, 1], 
           hover_name=speeches['text'].index, 
           color=speeches['text'].index.str.split(', ').str[-1].astype(int),
           color_continuous_scale='Turbo',
           size_max=12,
           size=[1] * np.ones(len(scores)))
fig.update_layout(xaxis_title='PC 1', 
                  yaxis_title='PC 2', 
                  title='PC 2 vs. PC 1 of TF-IDF-encoded<br>Presidential Speeches',
                  width=1000, height=600)

Summary

• One way to turn text, like 'big big big big data class', into numbers, is to count the number of occurrences of each word in the document, ignoring order. This is done using the bag of words model.
• Term frequency-inverse document frequency (TF-IDF) is a statistic that tries to quantify how important a term (word) is to a document. It balances:
  • how often a term appears in a particular document, $\text{tf}(t, d)$, with
  • how often a term appears across documents, $\text{idf}(t)$.
  • For a given document, the word with the highest TF-IDF is thought to "best summarize" that document.
• Both the bag of words model and TF-IDF are ways of converting texts to vector representations.
• To measure the similarity of two texts, convert the texts to their vector representations, and use cosine similarity.