In [1]:
from lec_utils import *
import matplotlib.pyplot as plt
from PIL import Image

Lecture 3¶

NumPy and Random Simulations¶

EECS 398: Practical Data Science, Winter 2025¶

practicaldsc.org • github.com/practicaldsc/wn25 • 📣 See latest announcements here on Ed

Agenda 📆¶

  • numpy arrays.
  • Multidimensional arrays and linear algebra.
  • Randomness and simulations.

See the end of Lecture 2 for a walkthrough video of the final area codes example; we won't touch on it today.

numpy arrays¶

Import statements¶

  • We use import statements to add the objects (values, functions, classes) defined in other modules to our programs. There are a few different ways to import.


Other terms I'll use for "module" are "library" and "package".

  • Option 1: import module.


Now, everytime we want to use a name in module, we must write module.<name>.

In [2]:
import math
In [3]:
math.sqrt(15)
Out[3]:
3.872983346207417
In [4]:
sqrt(15)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[4], line 1
----> 1 sqrt(15)

NameError: name 'sqrt' is not defined
  • Option 2: import module as m.


Now, everytime we want to use a name in module, we can write m.<name> instead of module.<name>.

In [5]:
# This is the standard way that we will import numpy.
import numpy as np
In [6]:
np.pi
Out[6]:
3.141592653589793
In [7]:
np.linalg.inv([[2, 1], 
               [3, 4]])
Out[7]:
array([[ 0.8, -0.2],
       [-0.6,  0.4]])
  • Option 3: from module import ....


This way, we explicitly state the names we want to import from module.
To import everything, write from module import *.

In [8]:
# Importing a particular function from the requests module.
from requests import get
In [9]:
# This typically fills up the namespace with a lot of unnecessary names, so use sparingly.
from math import *
In [10]:
sqrt
Out[10]:
<function math.sqrt(x, /)>

NumPy¶

No description has been provided for this image
  • NumPy (pronounced "num pie") is a Python library (module) that provides support for arrays and operations on them.
  • The pandas library, which we will use for tabular data manipulation, works in conjunction with numpy.
  • To use numpy, we need to import it. It's usually imported as np (but doesn't have to be!)
    We also had to install it on your computer first, but you already did that when you set up your environment.
In [11]:
import numpy as np

Arrays¶

  • The core data structure in numpy is the array. Moving forward, "array" will always refer to a numpy array.
  • One way to instantiate an array is to pass a list as an argument to the function np.array.
In [12]:
np.array([4, 9, 1, 2])
Out[12]:
array([4, 9, 1, 2])
  • Arrays, unlike lists, must be homogenous – all elements must be of the same type.
In [13]:
# All elements are converted to strings!
np.array([1961, 'michigan'])
Out[13]:
array(['1961', 'michigan'], dtype='<U21')

Array-number arithmetic¶

  • Arrays make it easy to perform the same operation to every element without a for-loop.
  • This behavior is formally known as "broadcasting", but we often say these operations are vectorized.
No description has been provided for this image
In [14]:
temps = [68, 72, 65, 64, 62, 61, 59, 64, 64, 63, 65, 62]
temps
Out[14]:
[68, 72, 65, 64, 62, 61, 59, 64, 64, 63, 65, 62]
In [15]:
temp_array = np.array(temps)
In [16]:
# Increase all temperatures by 3 degrees.
temp_array + 3
Out[16]:
array([71, 75, 68, 67, 65, 64, 62, 67, 67, 66, 68, 65])
In [17]:
# Halve all temperatures.
temp_array / 2
Out[17]:
array([34. , 36. , 32.5, 32. , 31. , 30.5, 29.5, 32. , 32. , 31.5, 32.5,
       31. ])
In [18]:
# Convert all temperatures to Celsius.
(5 / 9) * (temp_array - 32)
Out[18]:
array([20.  , 22.22, 18.33, 17.78, 16.67, 16.11, 15.  , 17.78, 17.78,
       17.22, 18.33, 16.67])
  • Note: In none of the above cells did we actually modify temp_array! Each of those expressions created a new array. To actually change temp_array, we need to reassign it to a new array.
In [19]:
temp_array
Out[19]:
array([68, 72, 65, 64, 62, 61, 59, 64, 64, 63, 65, 62])
In [20]:
temp_array = (5 / 9) * (temp_array - 32)
In [21]:
# Now in Celsius!
temp_array
Out[21]:
array([20.  , 22.22, 18.33, 17.78, 16.67, 16.11, 15.  , 17.78, 17.78,
       17.22, 18.33, 16.67])

⚠️ The dangers of unnecessary for-loops¶

  • Under the hood, numpy is implemented in C and Fortran, which are compiled languages that are much faster than Python. As a result, these vectorized operations are much quicker than if we used a vanilla Python for-loop.
    Also, the fact that arrays must be homogenous lend themselves to more efficient representations in memory.
  • We can time code in a Jupyter Notebook. Let's try and square a long sequence of integers and see how long it takes with a Python loop:
In [22]:
%%timeit
squares = []
for i in range(1_000_000):
    squares.append(i * i)

29.1 ms ± 270 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)
  • In vanilla Python, this takes about 0.03 seconds per loop.
    In numpy:
In [23]:
%%timeit
squares = np.arange(1_000_000) ** 2

808 μs ± 20.5 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
  • Only takes about 0.0008 seconds per loop, approximately 40x faster!

Element-wise arithmetic¶

  • We can apply arithmetic operations to multiple arrays, provided they have the same length.
  • The result is computed element-wise, which means that the arithmetic operation is applied to one pair of elements from each array at a time.
No description has been provided for this image
In [24]:
a = np.array([4, 5, -1])
b = np.array([2, 3, 2])
In [25]:
a + b
Out[25]:
array([6, 8, 1])
In [26]:
a / b
Out[26]:
array([ 2.  ,  1.67, -0.5 ])
In [27]:
a ** 2 + b ** 2
Out[27]:
array([20, 34,  5])

Array methods¶

  • Arrays come equipped with several handy methods; some examples are below, but you can read about them all here.
In [28]:
arr = np.array([3, 8, 4, -3.2])
In [29]:
(2 ** arr).sum()
Out[29]:
280.108818820412
In [30]:
(2 ** arr).mean()
Out[30]:
70.027204705103
In [31]:
(2 ** arr).max()
Out[31]:
256.0
In [32]:
(2 ** arr).argmax()
Out[32]:
1
In [33]:
# An attribute, not a method.
arr.shape
Out[33]:
(4,)

Question 🤔 (Answer at practicaldsc.org/q)

What questions do we have about arrays so far?

Activity

🎉 Congrats! 🎉 You won the lottery 💰. Here's how your payout works: on the first day of September, you are paid \$0.01. Every day thereafter, your pay doubles, so on the second day you're paid \$0.02, on the third day you're paid \$0.04, on the fourth day you're paid \$0.08, and so on.

September has 30 days.

Write a one-line expression that uses the numbers 2 and 30, along with the function np.arange and at least one array method, that computes the total amount in dollars you will be paid in September. No for-loops or list comprehensions allowed!


We have a 🎥 walkthrough video of this problem, but don't watch it until you've tried it yourself!

In [34]:
(2 ** np.arange(30) / 100).sum()
Out[34]:
10737418.23

Boolean filtering¶

  • Comparisons with arrays yield Boolean arrays! These can be used to answer questions about the values in an array.
In [35]:
temp_array
Out[35]:
array([20.  , 22.22, 18.33, 17.78, 16.67, 16.11, 15.  , 17.78, 17.78,
       17.22, 18.33, 16.67])
In [36]:
temp_array >= 18
Out[36]:
array([ True,  True,  True, False, False, False, False, False, False,
       False,  True, False])
  • How many values are greater than or equal to 18?
In [37]:
(temp_array >= 18).sum()
Out[37]:
4
In [38]:
np.count_nonzero(temp_array >= 18)
Out[38]:
4
  • What fraction of values are greater than or equal to 18?
In [39]:
(temp_array >= 18).mean()
Out[39]:
0.3333333333333333
  • Which values are greater than or equal to 18?
In [40]:
temp_array[temp_array >= 18]
Out[40]:
array([20.  , 22.22, 18.33, 18.33])
  • Which values are between 18 and 20?
In [41]:
# Note the parentheses!
temp_array[(temp_array >= 18) & (temp_array <= 20)]
Out[41]:
array([20.  , 18.33, 18.33])
In [42]:
# WRONG!
temp_array[(temp_array >= 18) and (temp_array <= 20)] 

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[42], line 2
      1 # WRONG!
----> 2 temp_array[(temp_array >= 18) and (temp_array <= 20)]

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

Note: & and | vs. and and or¶

  • In Python, the standard symbols for "and" and "or" are, literally, and and or.
In [43]:
if (5 > 3 and 'h' + 'i' == 'hi') or (-2 > 0):
    print('success')

success
  • But, when taking the element-wise and/or of two arrays, the standard operators don't work.
    Instead, use the bitwise operators: & for "and", | for "or".
In [44]:
temp_array
Out[44]:
array([20.  , 22.22, 18.33, 17.78, 16.67, 16.11, 15.  , 17.78, 17.78,
       17.22, 18.33, 16.67])
In [45]:
# Don't forget parentheses when using multiple conditions!
temp_array[(temp_array % 2 == 0) | (temp_array == temp_array.min())]
Out[45]:
array([20., 15.])
  • Read more about these differences here.

Multidimensional arrays and linear algebra¶

Multidimensional arrays¶

  • A matrix can be represented in code using a two dimensional (2D) array.
  • 2D arrays also resemble tables, or DataFrames, so it's worthwhile to study how they work.
In [46]:
nums = np.array([
    [5, 1, 9, 7],
    [9, 8, 2, 3],
    [2, 5, 0, 4]
])
nums
Out[46]:
array([[5, 1, 9, 7],
       [9, 8, 2, 3],
       [2, 5, 0, 4]])
In [47]:
# nums has 3 rows and 4 columns.
nums.shape
Out[47]:
(3, 4)
  • In addition to creating 2D arrays from scratch, we can also create 2D arrays by reshaping other arrays.
In [48]:
# Here, we're asking to reshape np.arange(1, 7)
# so that it has 2 rows and 3 columns.
a = np.arange(1, 7).reshape((2, 3)) 
a
Out[48]:
array([[1, 2, 3],
       [4, 5, 6]])

Operations along axes¶

  • In 2D arrays (and DataFrames), axis 0 refers to the rows (up and down) and axis 1 refers to the columns (left and right).
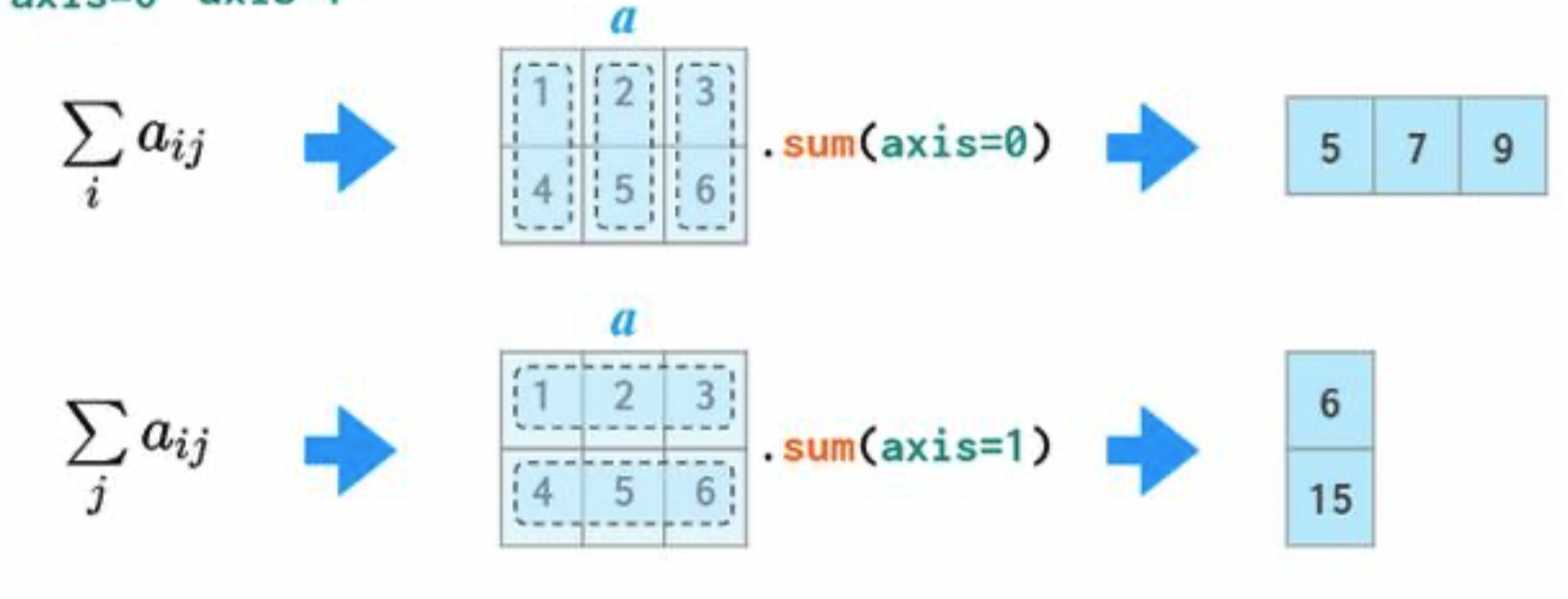
No description has been provided for this image
In [49]:
a
Out[49]:
array([[1, 2, 3],
       [4, 5, 6]])
  • If we specify axis=0, a.sum will "compress" along axis 0.
In [50]:
a.sum(axis=0)
Out[50]:
array([5, 7, 9])
  • If we specify axis=1, a.sum will "compress" along axis 1.
In [51]:
a.sum(axis=1)
Out[51]:
array([ 6, 15])

Selecting rows and columns from 2D arrays¶

  • You can use [square brackets] to slice rows and columns out of an array, too.
  • The general convention is:
array[<row positions>, <column positions>]
In [52]:
a
Out[52]:
array([[1, 2, 3],
       [4, 5, 6]])
In [53]:
# Accesses row 0 and all columns.
a[0, :]
Out[53]:
array([1, 2, 3])
In [54]:
# Same as the above.
a[0]
Out[54]:
array([1, 2, 3])
In [55]:
# Accesses all rows and column 1.
a[:, 1]
Out[55]:
array([2, 5])
In [56]:
# Access all rows and columns 0 and 2.
a[:, [0, 2]]
Out[56]:
array([[1, 3],
       [4, 6]])
In [57]:
# Accesses row 0 and columns 1 and onwards.
a[0, 1:]
Out[57]:
array([2, 3])

Activity

Suppose we run the cell below. 
s = (5, 3)
grid = np.ones(s) * 2 * np.arange(1, 16).reshape(s)
grid[-1, 1:].sum()

What is the output of the cell? Try and answer without writing any code. See the annotated slides for the solution.

In [ ]:
In [ ]:

Example: Image processing¶

  • Images can be represented as 3D numpy arrays.
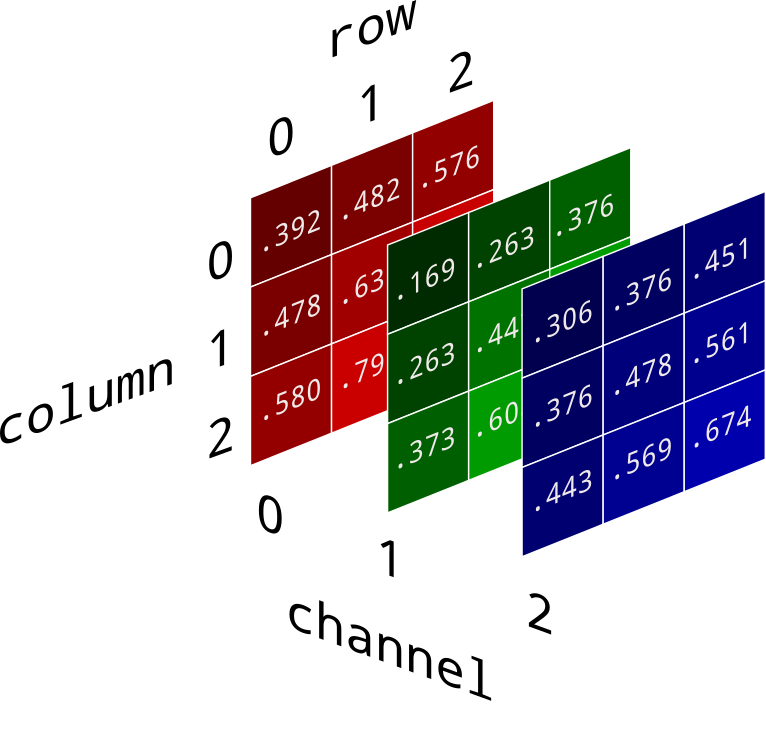No description has been provided for this image(image source)
  • The color of each pixel can be described with three numbers under the RGB model – a red value, green value, and blue value. Each of these can vary from 0 (least intensity) to 255 (most intensity).
    Experiment with RGB colors here.
In [58]:
img = np.asarray(Image.open('imgs/junior.jpeg'))
img
Out[58]:
array([[[ 98,  62,  46],
        [ 89,  56,  39],
        [ 88,  56,  41],
        ...,
        [123,  78,  59],
        [125,  78,  60],
        [128,  81,  63]],

       [[ 96,  60,  44],
        [ 89,  56,  39],
        [ 89,  57,  42],
        ...,
        [124,  79,  60],
        [125,  78,  60],
        [127,  80,  62]],

       [[ 94,  58,  42],
        [ 89,  56,  39],
        [ 89,  57,  42],
        ...,
        [125,  78,  60],
        [125,  78,  60],
        [126,  79,  61]],

       ...,

       [[ 89,  50,  11],
        [ 85,  46,   7],
        [ 81,  42,   3],
        ...,
        [ 94,  68,  33],
        [100,  74,  39],
        [108,  82,  47]],

       [[ 86,  48,  11],
        [ 84,  46,   9],
        [ 84,  46,   9],
        ...,
        [ 92,  66,  31],
        [100,  74,  39],
        [111,  85,  50]],

       [[ 94,  56,  19],
        [ 93,  55,  18],
        [ 95,  57,  21],
        ...,
        [ 90,  64,  29],
        [ 98,  72,  37],
        [112,  86,  51]]], dtype=uint8)
In [59]:
img.shape
Out[59]:
(2048, 1536, 3)
In [60]:
plt.imshow(img)
plt.axis('off');
No description has been provided for this image

Applying a grayscale filter¶

  • One way to convert an image to grayscale is to average its red, green, and blue values.
In [61]:
mean_2d = img.mean(axis=2) 
mean_2d
Out[61]:
array([[68.67, 61.33, 61.67, ..., 86.67, 87.67, 90.67],
       [66.67, 61.33, 62.67, ..., 87.67, 87.67, 89.67],
       [64.67, 61.33, 62.67, ..., 87.67, 87.67, 88.67],
       ...,
       [50.  , 46.  , 42.  , ..., 65.  , 71.  , 79.  ],
       [48.33, 46.33, 46.33, ..., 63.  , 71.  , 82.  ],
       [56.33, 55.33, 57.67, ..., 61.  , 69.  , 83.  ]])
In [62]:
# This is just a single red channel!
plt.imshow(mean_2d.astype(int))
plt.axis('off');
No description has been provided for this image
  • We need to repeat mean_2d three times along axis 2, to use the same values for the red, green, and blue channels. np.repeat will help us here.
In [63]:
# np.newaxis is an alias for None.
# It helps us introduce an additional axis.
np.arange(5)[:, np.newaxis]
Out[63]:
array([[0],
       [1],
       [2],
       [3],
       [4]])
In [64]:
np.repeat(np.arange(5)[:, np.newaxis], 3, axis=1)
Out[64]:
array([[0, 0, 0],
       [1, 1, 1],
       [2, 2, 2],
       [3, 3, 3],
       [4, 4, 4]])
In [65]:
mean_3d = np.repeat(mean_2d[:, :, np.newaxis], 3, axis=2).astype(int) 
mean_3d
Out[65]:
array([[[68, 68, 68],
        [61, 61, 61],
        [61, 61, 61],
        ...,
        [86, 86, 86],
        [87, 87, 87],
        [90, 90, 90]],

       [[66, 66, 66],
        [61, 61, 61],
        [62, 62, 62],
        ...,
        [87, 87, 87],
        [87, 87, 87],
        [89, 89, 89]],

       [[64, 64, 64],
        [61, 61, 61],
        [62, 62, 62],
        ...,
        [87, 87, 87],
        [87, 87, 87],
        [88, 88, 88]],

       ...,

       [[50, 50, 50],
        [46, 46, 46],
        [42, 42, 42],
        ...,
        [65, 65, 65],
        [71, 71, 71],
        [79, 79, 79]],

       [[48, 48, 48],
        [46, 46, 46],
        [46, 46, 46],
        ...,
        [63, 63, 63],
        [71, 71, 71],
        [82, 82, 82]],

       [[56, 56, 56],
        [55, 55, 55],
        [57, 57, 57],
        ...,
        [61, 61, 61],
        [69, 69, 69],
        [83, 83, 83]]])
In [66]:
plt.imshow(mean_3d)
plt.axis('off');
No description has been provided for this image

Reference Slide¶

Applying a sepia filter¶

We won't walk through this example in lecture, but it's here for your reference.

  • Let's sepia-fy Junior!
No description has been provided for this image (Image credits)
  • From here, we can apply this conversion to each pixel.
$$\begin{align*} R_{\text{sepia}} &= 0.393R + 0.769G + 0.189B \\ G_{\text{sepia}} &= 0.349R + 0.686G + 0.168B \\ B_{\text{sepia}} &= 0.272R + 0.534G + 0.131B\end{align*}$$
In [67]:
sepia_filter = np.array([
    [0.393, 0.769, 0.189],
    [0.349, 0.686, 0.168],
    [0.272, 0.534, 0.131]
])
In [68]:
# Multiplies each pixel by the sepia_filter matrix.
# Then, clips each RGB value to be between 0 and 1.
filtered = (img @ sepia_filter.T).clip(0, 255).astype(int)
filtered
Out[68]:
array([[[ 94,  84,  65],
        [ 85,  76,  59],
        [ 85,  76,  59],
        ...,
        [119, 106,  82],
        [120, 107,  83],
        [124, 110,  86]],

       [[ 92,  82,  63],
        [ 85,  76,  59],
        [ 86,  77,  60],
        ...,
        [120, 107,  83],
        [120, 107,  83],
        [123, 109,  85]],

       [[ 89,  79,  62],
        [ 85,  76,  59],
        [ 86,  77,  60],
        ...,
        [120, 107,  83],
        [120, 107,  83],
        [121, 108,  84]],

       ...,

       [[ 75,  67,  52],
        [ 70,  62,  48],
        [ 64,  57,  44],
        ...,
        [ 95,  84,  66],
        [103,  92,  71],
        [114, 101,  79]],

       [[ 72,  64,  50],
        [ 70,  62,  48],
        [ 70,  62,  48],
        ...,
        [ 92,  82,  64],
        [103,  92,  71],
        [118, 105,  82]],

       [[ 83,  74,  57],
        [ 82,  73,  57],
        [ 85,  75,  59],
        ...,
        [ 90,  80,  62],
        [100,  89,  69],
        [119, 106,  83]]])
In [69]:
plt.imshow(filtered)
plt.axis('off');
No description has been provided for this image

Matrix multiplication¶

  • In the coming weeks, we'll start to rely more and more on tools from linear algebra.
    You'll need this in Homework 2!
  • Suppose the matrix $A$ and vectors $\vec x$ and $\vec y$ are defined as follows:
$$A = \begin{bmatrix} 2 & -5 & 1 \\ 0 & 3 & 2 \end{bmatrix} \qquad \vec x = \begin{bmatrix} 1 \\ -1 \\ 4 \end{bmatrix} \qquad \vec y = \begin{bmatrix} 3 \\ -2 \end{bmatrix}$$
In [70]:
A = np.array([[2, -5, 1],
              [0,  3, 2]])
x = np.array([[1],
              [-1],
              [4]])
y = np.array([[3],
              [-2]])
  • We can use numpy to compute various quantities involving $A$, $\vec x$, and $\vec y$.
    For instance, what is the result of the product $A \vec x$?
    See the annotated slides for the math worked out.
In [71]:
A @ x
Out[71]:
array([[11],
       [ 5]])
  • What is the result of the product $A^T \vec y$?
In [72]:
A.T @ y
Out[72]:
array([[  6],
       [-21],
       [ -1]])
  • What is the result of the product $\vec x^T A^T A \vec x$?
In [73]:
x.T @ A.T @ A @ x
Out[73]:
array([[146]])

Example: Fibonacci numbers¶

  • The sequence of Fibonacci numbers,

    $$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...$$

    can be computed using matrix multiplication!

  • It can be shown (with induction!) that if $f_1 = 1$, $f_2 = 1$, and $f_{n} = f_{n - 1} + f_{n - 2}, n \geq 2$, then:
$$\begin{bmatrix} f_{n + 1} & f_n \\ f_n & f_{n - 1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n$$
In [74]:
fib = np.array([[1, 1],
                [1, 0]])
In [75]:
np.linalg.matrix_power(fib, 8)
Out[75]:
array([[34, 21],
       [21, 13]])

Key takeaway: avoid for-loops whenever possible!¶

You can do a lot without for-loops, both in numpy and in pandas.

Randomness and simulations¶

np.random¶

  • The submodule np.random contains various functions that produce random results.
    These use pseudo-random number generators to generate random-seeming sequences of results.
  • np.random.random returns a real number drawn at random from the interval [0, 1].
In [76]:
np.random.random()
Out[76]:
0.004201413524692388
  • np.random.randint returns a random integer in the specified range.
    In the example below, between 1 and 6, inclusive.
In [77]:
# Run this cell multiple times!
np.random.randint(1, 7)
Out[77]:
2

Random sampling¶

  • np.random.choice and np.random.multinomial allow us to draw random samples.
  • np.random.choice returns randomly selected element(s) from the provided sequence.
    By default, this is done with replacement, but it can be done without replacement, too.
In [78]:
unique_names = np.load('data/wn25-names.npy')
unique_names
Out[78]:
array(['Aayush', 'Abby', 'Abhinav', ..., 'Yun', 'Zhicong', 'Zijie'],
      dtype='<U10')
In [79]:
# Returns a randomly selected element from the provided array, 5 times, with replacement.
# The resulting array COULD have duplicates.
np.random.choice(unique_names, 5)
Out[79]:
array(['Tanish', 'Sanya', 'Xingzhi', 'Haoyan', 'Kovidh'], dtype='<U10')
In [80]:
# Returns a randomly selected element from the provided array, 5 times, without replacement.
# The resulting array CANNOT have duplicates.
np.random.choice(unique_names, 5, replace=False)
Out[80]:
array(['Amy', 'In', 'Kiran', 'Xingzhi', 'Caleb'], dtype='<U10')
  • np.random.multinomial returns the result of drawing a sample from a multinomial distribution.
    For instance, the cell below simulates the number of marbles of each color drawn from a bag in which 30% are blue, 50% are orange, and 20% are purple, and 15 marbles are drawn with replacement.
In [81]:
np.random.multinomial(15, [0.3, 0.5, 0.2])
Out[81]:
array([6, 6, 3])

Simulations¶

  • Often, we'll want to estimate the probability of an event, but it may not be possible – or we may not know how – to calculate the probability exactly.
    e.g., the probability that I see between 40 and 50 heads when I flip a fair coin 100 times.
  • Or, we may have a theoretical answer, and want to validate it using another approach.
  • In such cases, we can use the power of simulation.
    We can repeat the experiment many, many times, compute the fraction of experiments in which our event occurs, and use this fraction as an estimate of the probability of our event.
    This is the basis of Monte Carlo Methods.
  • Theory tells us that the more repetitions we perform of our experiment, the closer our fraction will be to the true probability of the event!


Specifically, the Law of Large Numbers tells us this.

Example: Coin flipping¶

  • Question: What is the probability that I see between 40 and 50 heads, inclusive, when I flip a fair coin 100 times?
  • To estimate this probability, we need to:
    • Flip 100 fair coins and write down the number of heads,
    • and repeat that process many, many times.
In [82]:
np.random.multinomial(100, [0.5, 0.5])
Out[82]:
array([54, 46])
In [83]:
np.random.multinomial(100, [0.5, 0.5], 100_000)
Out[83]:
array([[55, 45],
       [50, 50],
       [53, 47],
       ...,
       [40, 60],
       [46, 54],
       [57, 43]])
In [84]:
# outcomes is an array with 100,000 elements,
# each of which is the number of heads in 100 simulated flips of a fair coin.
outcomes = np.random.multinomial(100, [0.5, 0.5], 100_000)[:, 0] 
outcomes
Out[84]:
array([51, 61, 53, ..., 53, 52, 52])

Estimating a probability from empirical results¶

In [85]:
px.histogram(outcomes, title='Number of Heads in 100 Simulated Flips of a Fair Coin')
  • Our estimated probability of seeing between 40 and 50 heads is the fraction (proportion) of experiments in which we saw between 40 and 50 heads:
In [86]:
((outcomes >= 40) & (outcomes <= 50)).mean()
Out[86]:
0.52122
  • This is remarkably close to the true, theoretical answer, which can be computed using the binomial distribution.
$$P(40 \leq \text{heads} \leq 50) = \sum_{k = 40}^{50} {100 \choose k} \frac{1}{2^{100}}$$
In [87]:
from scipy.special import comb
sum([comb(100, k) for k in range(40, 51)]) / (2 ** 100)
Out[87]:
0.5221945185847369

Question 🤔 (Answer at practicaldsc.org/q)

What questions do you have about our coin flipping simulation?

Example: Airplane seats ✈️¶

  • A permutation of a sequence is a reshuffling of its elements.
    np.random.permutation returns a permutation of the specified sequence.
In [88]:
np.random.permutation(['A', 'B', 'C'])
Out[88]:
array(['B', 'C', 'A'], dtype='<U1')
  • Suppose a flight on Wolverine Airlines is scheduled for $n$ passengers, all of whom have an assigned seat.
  • The airline loses track of seat assignments and everyone sits in a random seat.
    What is the probability that nobody is in their originally assigned seat?

Simulating airplane seats¶

  • Let's first simulate one hypothetical "plane".
In [89]:
def simulate_one_plane(n, display=False):
    """Simulates one plane of n people.
       Returns True if nobody is in their originally assigned seat,
       or False if at least one person is.
    """
    poss = np.arange(1, n + 1)
    shuffled = np.random.permutation(poss)
    if display:
        print('Real plane:     ', poss)
        print('Simulated plane:', shuffled)
    return (poss != shuffled).all()
simulate_one_plane(10, display=True)

Real plane:      [ 1  2  3  4  5  6  7  8  9 10]
Simulated plane: [10  2  6  3  1  9  5  8  4  7]
Out[89]:
False
  • Now, let's call simulate_one_plane many, many times and compute the proportion of calls that return True.
    We'll arbitrarily start with $n = 50$, but change it and see what happens to the answer!
In [90]:
n = 50
prob = np.mean([simulate_one_plane(n) for _ in range(100_000)]) 
prob
Out[90]:
0.36961

Airplane seats, solved¶

  • The probability that nobody is in their originally assigned seat is:
$$P(\text{nobody in assigned seat, $n$ passengers}) = 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \frac{1}{4!} - ... \frac{1}{n!}$$
  • Fact: As $n \rightarrow \infty$, this approaches:
$$P(\text{nobody in assigned seat, $n$ passengers}) \rightarrow \frac{1}{e}$$
In [91]:
1 / np.e
Out[91]:
0.36787944117144233

Curious to learn more?¶

  • Watch the following video by Numberphile, a popular YouTube channel for math-related content.
In [92]:
YouTubeVideo('pbXg5EI5t4c')
Out[92]:
  • Simulations are powerful!

What's next?¶

  • There is no lecture on Monday, due to MLK Day.
  • In Lecture 4 next Wednesday, we'll do a deep dive into pandas DataFrames.
  • Homework 2, which will be released by Saturday, will contain some content from today's lecture and some content from Lecture 4.