# Run this cell to get everything set up.
from lec_utils import *
import lec27_util as util

import warnings
warnings.simplefilter('ignore')

Lecture 27

Computer Vision, Conclusion

EECS 398-003: Practical Data Science, Fall 2024

practicaldsc.org • github.com/practicaldsc/fa24

Announcements 📣

• Homework 11 is cancelled – everyone will receive 100% on it!

• The Portfolio Homework is due on Saturday, and slip days are not allowed!
  Remember to submit both your notebook PDF and the link to your website.
  There's a remote office hour on Saturday!

• The optional, extra credit prediction competition in Homework 10 is open until Monday.

• If at least 85% of the class fills out both:

  • This internal End-of-Semester Survey, and
  • the Official Campus Evaluations,
    

  then we will add 1% of extra credit to everyone's overall grade.
  
  Deadline: Tuesday, December 10th at 11:59PM.

• Discussion tomorrow is replaced with office hours (in the regular discussion section rooms and times).

Final exam details 🙇

• The Final Exam is on Thursday, December 12th from 4-6PM.
  You'll receive your assigned room via email by Monday.

• 25-35% of the questions will be about pre-midterm content; the rest will be about post-midterm content.
  All questions on the exam will count towards your final exam score. See the Redemption Policy in the syllabus.

• You can bring 2 double-sided handwritten notes sheets.
  Feel free to bring your midterm notes sheet as one of your two sheets!

• We have two review sessions next week, one on Monday from 6:30-8:30PM (pre-midterm content) and one on Tuesday from 5-7PM (post-midterm content), both in 1670 BBB.
  Both will be recorded. Format TBD, but if we know in advance which problems we plan to cover, we'll let you know over the weekend so you can come prepared.

• See this post on Ed for some studying tips.
  The study site is the most important resource, followed by lecture slides, and then assignments.

Agenda

• Reflection 🤔.
• Computer vision 👾.
• Parting thoughts 💭.

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

Reflection 💭

---

From Lecture 1: Topics

• Week 1: Python and Jupyter Notebooks.
• Weeks 2-3: numpy, pandas, and Exploratory Data Analysis.
• Weeks 4-5: Missing Data; Web Scraping and APIs.
• Weeks 5-6: Text Processing.
• Week 7: Midterm Exam.
• Weeks 8-10: Linear Regression through Linear Algebra.
• Weeks 11-12: Generalization, Regularization, and Cross-Validation.
• Weeks 12-14: Gradient Descent and Logistic Regression.
• Weeks 15-16: Unsupervised Learning, Final Exam.

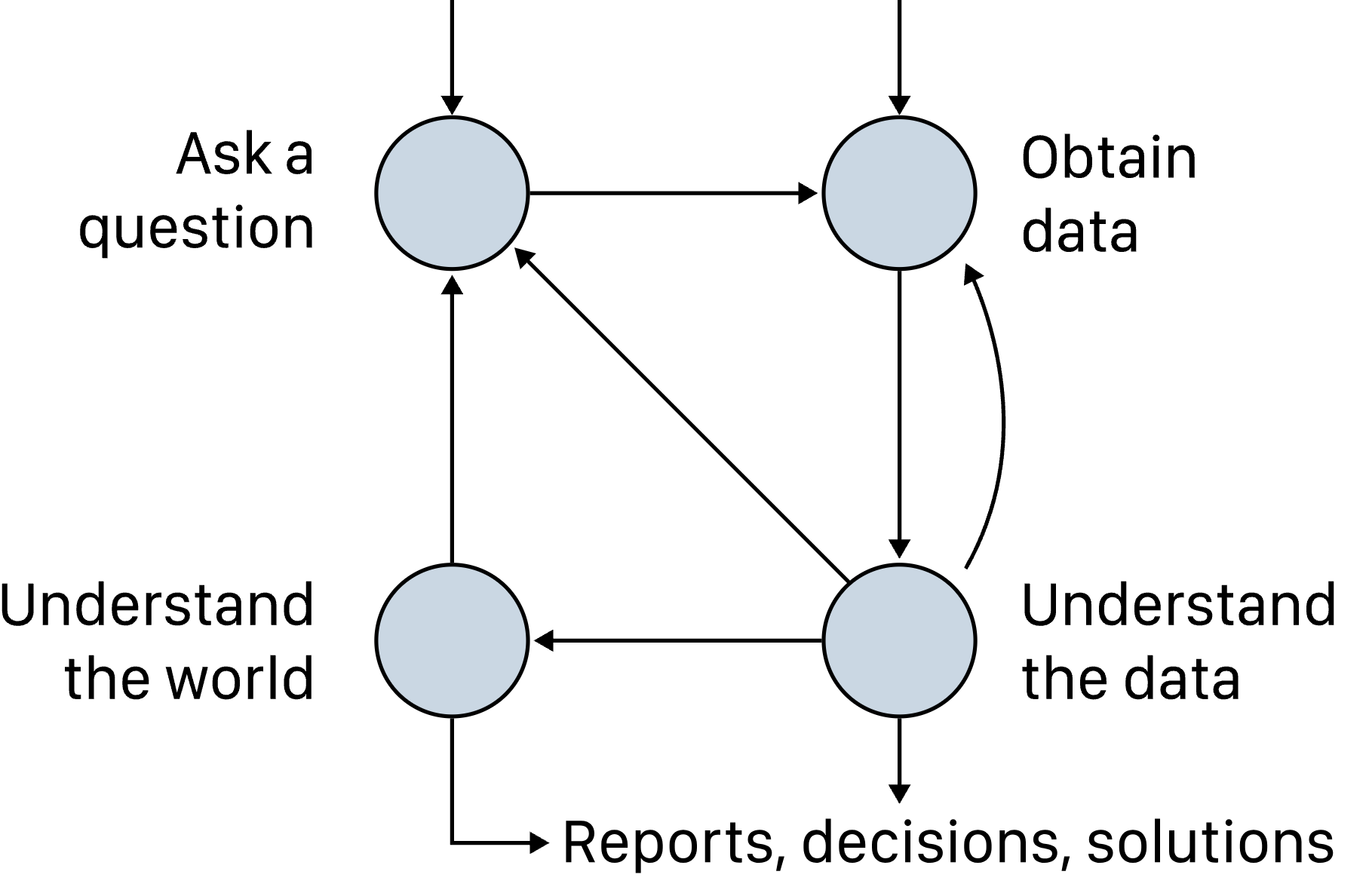
The data science lifecycle, which we've revisited repeatedly throughout the semester.

You've accomplished a lot!

• You learned a lot this semester – you're now among the most qualified data scientists in the world!

• You're now able to start with raw data and come up with accurate, meaningful insights that you can share with others.

• You know how to use industry-standard data manipulation tools, and you understand the inner-workings of complicated statistical models.

• You're well-prepared for internships and data science interviews, ready to create your own portfolio of personal projects, and have the background and maturity to succeed in more advanced data science-adjacent courses.

What's next?

• Data science is a relatively new, rapidly evolving field, so you'll need to keep evolving with it.

• Fun fact: One of the earliest uses of the term data science in a lecture given here at U–M in 1997 by former statistics and IOE Professor C.F. Jeff Wu:

  In his 1997 inaugural lecture for the Carver Chair , he coined the term data science and advocated that statistics be renamed data science and statistician to data scientist. (source)

• The tools of the trade may change, but the core principles won't – you now have a strong foundation on which you can develop new skills.

Computer vision 👾

---

We'll wrap up the semester by looking at a fun application area of the tools we've seen – computer vision. None of the new material today is in scope for the exam, but a lot of it is implicitly review.

Goal: Given an image of a digit, classify the digit as either 0, 1, 2, 3, 4, 5, 6, 7, 8, or, 9.

This is a multi-class classification problem with 10 classes.

This is also an example of computer vision,
a branch of machine learning that deals with learning patterns in images and videos.

The MNIST dataset

• The MNIST dataset contains 70,000 labeled images of digits, all of which are 28 pixels by 28 pixels and grayscale (no color).
  MNIST stands for "Modified National Institute of Standards and Technology". Yann LeCun et. al. are responsible for curating the dataset, read the original webpage for it here.

• The dataset is pre-split into a training set of 60,000 images and test set of 10,000 images.

• Test set performance on MNIST is a common benchmark for evaluating the quality of a classifier.
  Convolutional neural networks, one of the most popular model architectures for computer vision, were developed specifically in the context of achieving high accuracy on MNIST.
  There are other, similarly-purposed datasets too, like FashionMNIST.

• State of the art neural network-based models have achieved test set accuracies of as high as 99.87%.
  See the leaderboard here!

Loading the data

• sklearn has a built-in function for loading datasets from OpenML.

from sklearn.datasets import fetch_openml
X, y = fetch_openml("mnist_784", version=1, return_X_y=True, as_frame=True)

# The documentation here: https://www.openml.org/search?type=data&status=active&id=554
# tells us that the first 60,000 rows constitute the training set.
X_train, X_test = X.iloc[:60000], X.iloc[60000:]
y_train, y_test = y.iloc[:60000].astype(int), y.iloc[60000:].astype(int)

• What do X_train and y_train actually look like?

X_train

	pixel1	pixel2	pixel3	pixel4	...	pixel781	pixel782	pixel783	pixel784
0	0	0	0	0	...	0	0	0	0
1	0	0	0	0	...	0	0	0	0
2	0	0	0	0	...	0	0	0	0
...	...	...	...	...	...	...	...	...	...
59997	0	0	0	0	...	0	0	0	0
59998	0	0	0	0	...	0	0	0	0
59999	0	0	0	0	...	0	0	0	0

60000 rows × 784 columns

y_train

0        5
1        0
2        4
        ..
59997    5
59998    6
59999    8
Name: class, Length: 60000, dtype: int64

From vectors to images

• In X_train, each image is represented by a $28 \cdot 28 = 784$-dimensional vector, representing a flattened version of the image.

X_train.iloc[98]

pixel1      0
pixel2      0
pixel3      0
           ..
pixel782    0
pixel783    0
pixel784    0
Name: 98, Length: 784, dtype: int64

• The first 28 pixels are the first row of the image, the second 28 pixels are the second row of the image, and so on. To view the image, we can reshape the vector into a 2D grid.

X_train.iloc[98].to_numpy().reshape((28, 28))

array([[0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0],
       ...,
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0]])

• Each pixel is represented with a value from 0 to 255, where larger values are more intense (darker in the plot below).

# We'll keep using image 98 as an example, so remember that it's a 3!
util.show_image(X_train.iloc[98])

The distribution of the training set

• Before training any models, we should assess whether there's any class imbalance in the training set.
  Remember, we shouldn't peek at the test set until we've actually trained a model!

y_train.value_counts(normalize=True).sort_index().plot(kind='bar', title='Distribution of Digits in the Training Set')

• The 10 possible digits seem to appear at roughly the same frequency.

Model #1: $k$-Nearest Neighbors 🏡🏠

• We can use $k$-nearest neighbors to predict the digit in a new image, $\vec{x}_\text{new} \in \mathbb{R}^{784}$.
  Intuitively, this means finding the $k$ "most similar" images to $\vec{x}_\text{new}$.
  Remember, $k$-nearest neighbors is a classification method for supervised learning!

• Since we're treating each image in our training set as a "flat" vector in $\mathbb{R}^{784}$, we're ignoring any spatial patterns in each image.

from sklearn.neighbors import KNeighborsClassifier

model_knn = KNeighborsClassifier(n_neighbors=100) # Arbitrary choice; remember, there are 60,000 points in the training set.
model_knn.fit(X_train, y_train)

KNeighborsClassifier(n_neighbors=100)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• Note that "training" a $k$-NN classifier (i.e. calling fit) is instant, because nearest neighbor models do all of their calculation upon calling predict.

• Calling predict is much slower than calling fit – for each input to predict, the model must find the distance between the input vector and all 60,000 vectors in the training set to see which $k=100$ are the closest.

model_knn.predict(X_train.iloc[[98]])

array([3])

# Accuracy on test set. Takes ~10 seconds on my computer, but is fairly high!
y_test_pred = model_knn.predict(X_test)
(y_test == y_test_pred).mean()

0.944

What kinds of errors does the model make?

• A 100-nearest neighbor classifier achieves 94.4% test set accuracy.

• To further understand the classifier's performance, we can draw its confusion matrix.

X_test_labeled = X_test.assign(
    true=y_test,
    pred=y_test_pred
)

util.show_confusion(y_test, y_test_pred, title='Confusion Matrix for 100-Nearest Neighbors Model')

• Some of the most common errors seem to be:
  • Predicting 1 when the true digit is 2 or 7.
  • Predicting 7 when the true digit is 2.
  • Predicting 9 when the true digit is 4 or 7.

• Let's peek at some of those cases!

Examining misclassified images

• Run the cell below repeatedly to see a randomly-chosen image from the test set that we classified incorrectly.

util.show_image_and_label(X_test_labeled.query('pred != true').sample().iloc[0])

• Run the cell below repeatedly to see a randomly-chosen image from the test set that we incorrectly classified as a 1.

util.show_image_and_label(X_test_labeled.query('pred != true and pred == 1').sample().iloc[0])

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

Downsides of $k$-nearest neighbors

• In the example below, our 100-nearest neighbor classifier predicted 1, when the true label was 2.

util.show_image_and_label(X_test_labeled.query('pred != true and pred == 1').iloc[1])

• One downside: $k$-nearest neighbors doesn't incorporate any probability in its decision-making process. What if we could get a probability that the above image is of a 0, 1, 2, 3, ..., 9?

• Another downside: Classifying a new image takes relatively long. What if we could learn patterns from the training set in advance, so that predicting new images is relatively quick?

What about logistic regression?

• As we've seen, in binary classification, logistic regression models the probability of belonging to class 1, given a feature vector $\vec{x}_i \in \mathbb{R}^{784}$:

$$P(y_i = 1 | \vec{x}_i) = \sigma (w_0 + w_1 x_i^{(1)} + w_2 x_i^{(2)} + ... + w_d x_i^{(d)}) = \sigma\left(\vec{w} \cdot \text{Aug}(\vec{x}_i) \right)$$

• In logistic regression, $y_i \in \{0, 1\}$. But, in our current image classification problem, $y_i \in \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$, so we can't use logistic regression directly.

• One idea: one-vs-rest. Fit 10 separate logistic regression models – one per class – and predict the class that has the highest probability.
  • Image is 0 vs. image is not 0.
  • Image is 1 vs. image is not 1.
  • ...
  • Image is 9 vs. image is not 9.

• Another idea: one-vs-one. Fit ${10 \choose 2} = 55$ separate logistic regression models – one per pair of classes – and predict the class that "wins" the most predictions.
  • Image is 0 vs. image is 1.
  • Image is 0 vs. image is 2.
  • ...
  • Image is 8 vs. image is 9.

• Let's try something slightly different than listed above.

Model #2: Multinomial logistic regression 📈

• Multinomial logistic regression, also known as softmax regression, models the probability of belonging to any class, given a feature vector $\vec x_i \in \mathbb{R}^{784}$.
  Think of it as a generalization of logistic regression.

• Multinomial logistic regression models the probability of each class directly, and then predicts the most likely class.
  Let $p_j$ represent the modelled probability of class $j$, given a feature vector. Note that $j \in \{0, 1, ..., 9\}$.
  Then, for instance:

$$p_0 = P(y_i = 0 | \vec{x}_i) = \frac{e^{\vec{w}_0 \cdot \text{Aug}(\vec{x}_i)}}{\sum_{j = 0}^9 e^{\vec{w}_j \cdot \text{Aug}(\vec{x})}}$$

$$p_3 = P(y_i = 3 | \vec{x}_i) = \frac{e^{\vec{w}_3 \cdot \text{Aug}(\vec{x}_i)}}{\sum_{j = 0}^9 e^{\vec{w}_j \cdot \text{Aug}(\vec{x})}}$$

$$p_k = P(y_i = k | \vec{x}_i) = \frac{e^{\vec{w}_k \cdot \text{Aug}(\vec{x}_i)}}{\sum_{j = 0}^9 e^{\vec w_j \cdot \text{Aug}(\vec x_i)}}$$

• Instead of a single parameter vector $\vec{w}$, there are 10 parameter vectors, $\vec w_0$, $\vec w_1$, ..., $\vec w_9$!

Aside: The softmax function

• The softmax function is a generalization of the logistic function to multiple dimensions.
  

Suppose $\vec z \in \mathbb{R}^d$. Then, the softmax of $\vec z$ is defined element-wise as follows:

$$\sigma(\vec z)_i = \frac{e^{z_i}}{\sum_{j = 1}^d e^{z_j}}$$

• For example, suppose $\vec{z} = \begin{bmatrix} -5 \\ 2 \\ 4 \end{bmatrix}$. Then:

$$\sigma(\vec z) = \begin{bmatrix} \sigma(\vec z)_1 \\ \sigma(\vec z)_2 \\ \sigma(\vec z)_3 \end{bmatrix} = \underbrace{\begin{bmatrix} \frac{e^{-5}}{e^{-5} + e^2 + e^4} \\ \frac{e^{2}}{e^{-5} + e^2 + e^4} \\ \frac{e^{4}}{e^{-5} + e^2 + e^4} \end{bmatrix}}_\text{note the constant denominator!} = \begin{bmatrix} 0.0001 \\ 0.1192 \\ 0.8807 \end{bmatrix}$$

• Why is it defined this way? It maps a vector of real numbers to a vector of probabilities!
  Note that the denominator, $\sum_{j=1}^d e^{z_j}$, normalizes the $e^{z_i}$ terms so that the results sum to 1.

• Multinomial logistic regression, i.e. softmax regression, trains 10 linear models of the form $\vec w_j \cdot \text{Aug}(\vec x_i)$ – one per class, $j$ – and feeds the output of each through the softmax function, so the results can be interpreted as probabilities.

  $$P(y_i = k | \vec{x}_i) = \frac{e^{\vec w_k \cdot \text{Aug}(\vec x_i)}}{\sum_{j = 0}^9 e^{\vec w_j \cdot \text{Aug}(\vec x_i)}}$$

  The 10 optimal parameter vectors, $\vec w_0^*$, $\vec w_1^*$, ..., $\vec w_9^*$, are chosen to minimize mean cross-entropy loss, just like before!

Multinomial logistic regression in sklearn

• The LogisticRegression class supports multinomial logistic regression.

from sklearn.linear_model import LogisticRegression
model_log = LogisticRegression(multi_class='multinomial', penalty='l1', solver='saga')
model_log

LogisticRegression(multi_class='multinomial', penalty='l1', solver='saga')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• Given that we have 60,000 training examples, each of which are 784-dimensional, training on the full training set takes quite a while – longer than we have time to run in lecture! Just to demonstrate, we'll fit on just the first 10,000 rows of the training set.

model_log.fit(X_train.head(10000), y_train.head(10000))

LogisticRegression(multi_class='multinomial', penalty='l1', solver='saga')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• While calling fit takes a while, calling predict is fast!

util.show_image(X_train.iloc[[98]])

model_log.predict(X_train.iloc[[98]])

array([3])

# MUCH faster than with the k-nearest neighbors model!
model_log.score(X_test, y_test)

0.9015

What kinds of errors does this model make?

• The our multinomial logistic regression model, trained on just the first 10,000 rows of the training set, achieves 90.12% test set accuracy.

• Let's peek at the confusion matrix once again.

X_test_labeled = X_test.assign(
    true=y_test,
    pred=model_log.predict(X_test)
)

util.show_confusion(y_test, model_log.predict(X_test), title='Confusion Matrix for Multinomial Logistic Regression Model')

• The most common types of errors are now different! Common errors:
  • Predicting 8 when the true digit is a 2 or 5.
  • Predicting 3 when the true digit is a 5 (or vice versa).

Modeling uncertainty

• Let's look at test set images that the multinomial logistic regression model misclassified.

util.show_image_and_label(X_test_labeled.query('pred != true and pred == 8').iloc[15])

• We can use predict_proba to see the distribution of predicted probabilities per class.

model_log.predict_proba(X_test_labeled.query('pred != true and pred == 8').iloc[[15], :-2])

array([[0.  , 0.  , 0.1 , 0.03, 0.  , 0.  , 0.  , 0.  , 0.86, 0.  ]])

util.visualize_probs(model_log.predict_proba(X_test_labeled.query('pred != true and pred == 8').iloc[[15], :-2]))

Other close calls

• Repeatedly run the cell below to look at the distribution of predicted probabilities for misclassified examples.

t = X_test_labeled.query('pred != true').reset_index(drop=True)
t = t.assign(second_highest_prob = pd.DataFrame(model_log.predict_proba(t.iloc[:, :-2])).apply(lambda r: r.sort_values().iloc[-2], axis=1))
p = t[t['second_highest_prob'] >= 0.3].sample().iloc[0]
util.show_image_and_label(p.iloc[:-1].astype(int)).show()
util.visualize_probs(model_log.predict_proba(p.iloc[:-3].to_frame().T))

Visualizing coefficients

• Since there are 10 classes, model_log has 10 parameter vectors (each in $\mathbb{R}^{784}$) – one per class.

model_log.coef_

array([[0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       ...,
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.]])

model_log.coef_.shape

(10, 784)

• We can visualize these coefficients, too!
  Below, pixels in blue had a positive coefficient, i.e. increase the probability of class 0. Pixels in red had a negative coefficient, i.e. decrease the probability of class 0.

px.imshow(model_log.coef_[0].reshape((28, 28)), color_continuous_scale='Rdbu', title='Class 0 Coefficients')

util.plot_model_coefficients(model_log.coef_)

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

Reflection

• We've fit two models to the MNIST training set so far:
  • $k$-nearest neighbors.
  • Multinomial logistic regression.

• Both models achieved a test set accuracy above 90%.

• Both models are slow in some sense:
  • $k$-nearest neighbors is slow at classifying new images.
  • Logistic regression is slow to train.

• These issues, in part, stem from the fact that our design matrix has $28 \cdot 28 = 784$ columns, i.e. 784 features:

X_train

	pixel1	pixel2	pixel3	pixel4	...	pixel781	pixel782	pixel783	pixel784
0	0	0	0	0	...	0	0	0	0
1	0	0	0	0	...	0	0	0	0
2	0	0	0	0	...	0	0	0	0
...	...	...	...	...	...	...	...	...	...
59997	0	0	0	0	...	0	0	0	0
59998	0	0	0	0	...	0	0	0	0
59999	0	0	0	0	...	0	0	0	0

60000 rows × 784 columns

• Is there a way we could reduce the number of features we use, i.e. reduce the number of columns in the design matrix, and still achieve decent test set performance?

Principal component analysis (PCA)

• Principal component analysis (PCA) is an unsupervised learning technique used for dimensionality reduction.

• It'll allow us to take:
  • X_train, which has 60,000 rows and 784 columns, and transform it into
  • X_train_approx, which has 60,000 rows and $p$ columns, where $p$ is as small as we want (e.g. $p = 2$).

• It creates $p$ new features, each of which is a linear combination of all existing 784 features.
  • That is, it does not just select $p$ of the original features! (Here, that would mean just looking at $p$ of the original pixels.)
  • These new features are chosen to capture as much variability (information) in the original data as possible.

• How? The details are out of scope for us, but it leverages the singular value decomposition from linear algebra:

$$X = U \Sigma V^T$$

PCA in sklearn

• sklearn has an implementation of PCA, which operates like a transformer.
  Remember, PCA is an unsupervised technique! We don't use the actual digit labels for each image when computing this transformation.

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
pca.fit(X_train)

PCA(n_components=2)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• Once fit, pca can transform X_train into a 2-column matrix in a way that retains the bulk of the information:

$$\mathbb{R}^{60000 \times 784} \rightarrow \mathbb{R}^{60000 \times 2}$$

X_train_approx = pca.transform(X_train)
X_train_approx.shape

(60000, 2)

X_train_approx

array([[ 123.93,  312.67],
       [1011.72,  294.86],
       [ -51.85, -392.17],
       ...,
       [-178.05, -160.08],
       [ 130.61,    5.59],
       [-173.44,   24.72]])

• When each data point was 784-dimensional, we couldn't visualize our training set.
  But now, each data point is 2-dimensional, which we can easily visualize with a scatter plot!

Visualizing principal components

• The new features that PCA creates are called principal components (PCs).
  Note that the principal component values no longer correspond to pixel intensities, which used to range between 0 and 255.

• Plotting PC 2 vs. PC 1 doesn't lead to a ton of insight:

util.show_2_pcs(X_train_approx, y_train)

Clusters in principal components

• But what if we color each point by its true class?

util.show_2_pcs(X_train_approx, y_train, color=True)

• Key idea: Even when projected onto just two principal components, the 0s tend to look alike, the 1s tend to look alike, and so on!

• This doesn't always happen when using PCA; use it as part of your exploratory data analysis toolkit.

PCA as a preprocessing step

• We can use PCA as part of a larger modeling pipeline. We've chosen a number of principal components to use in advance, but in practice we should cross-validate.

$$\text{raw data in }\mathbb{R}^{60000 \times 784} \rightarrow \text{transformed data in }\mathbb{R}^{60000 \times 30} \rightarrow \text{predicted probabilities}$$

from sklearn.pipeline import make_pipeline

model_pca_log = make_pipeline(
    PCA(n_components=30),
    LogisticRegression(multi_class='multinomial', penalty='l1', solver='saga')
)
model_pca_log

Pipeline(steps=[('pca', PCA(n_components=30)),
                ('logisticregression',
                 LogisticRegression(multi_class='multinomial', penalty='l1',
                                    solver='saga'))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• The transformed data is of a much lower dimension than the raw data. As a result, we can train – and predict – on the full training set very quickly!

model_pca_log.fit(X_train, y_train)

Pipeline(steps=[('pca', PCA(n_components=30)),
                ('logisticregression',
                 LogisticRegression(multi_class='multinomial', penalty='l1',
                                    solver='saga'))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• And the test set accuracy is still good!

model_pca_log.score(X_test, y_test)

0.8869

Parting thoughts 👋

---

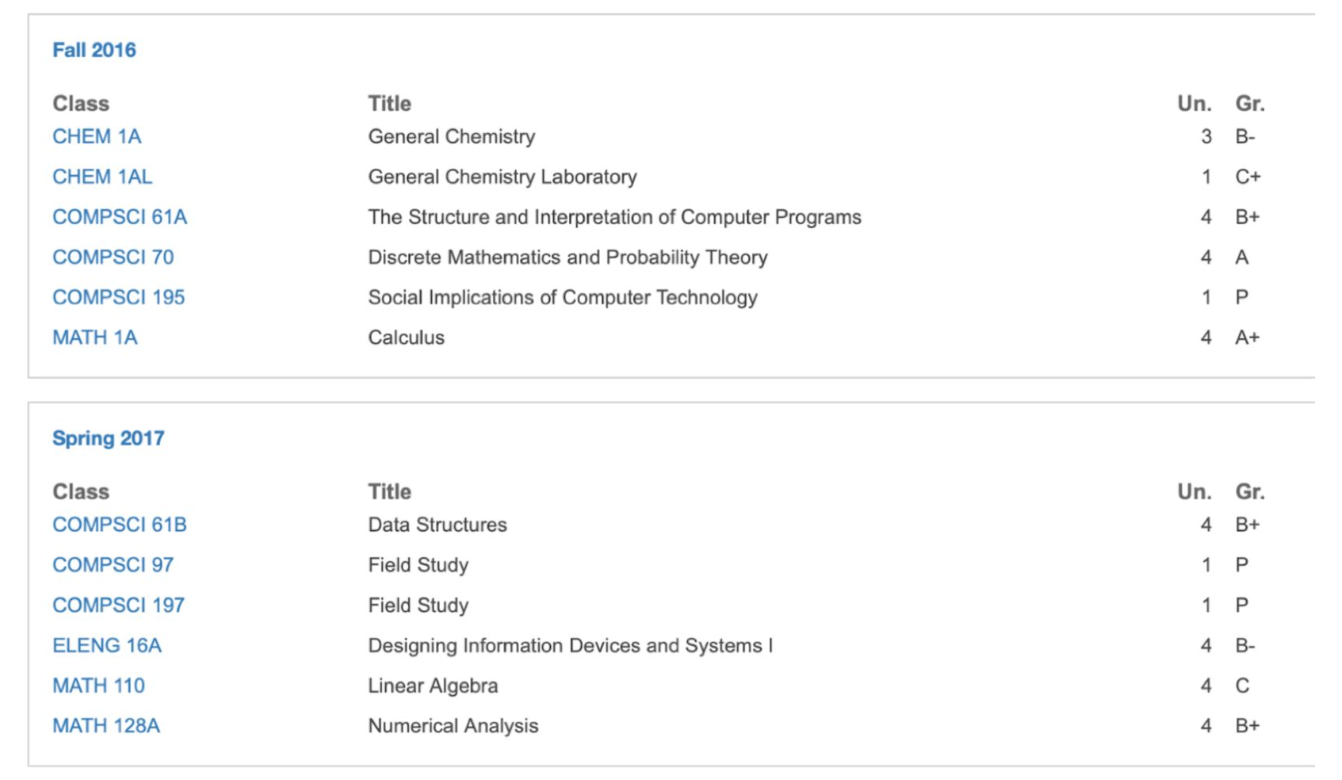
Suraj's freshman year transcript.

Thank you, and keep in touch!

• Thank you for signing up for this brand-new class!

• The course would not have been possible without our GSIs, IAs, and readers: Nishant Kheterpal, Yutong Li, Pranavi Pratapa, Neeru Uppalapati, Tahseen Younus, and Jingrui Zhang.

• Don't be a stranger – our contact information is at practicaldsc.org/staff. We want to hear about what you do after this class.
  This quarter's course website will remain online permanently, so you can refer back to the content.