# Run this cell to get everything set up.
from lec_utils import *
import lec26_util as util
from ipywidgets import interact
import warnings
warnings.simplefilter('ignore')

Lecture 26

Clustering

EECS 398-003: Practical Data Science, Fall 2024

practicaldsc.org • github.com/practicaldsc/fa24

Announcements 📣

• Homework 11 is cancelled – everyone will receive 100% on it!
• If you're still working on Homework 10, make sure to read #346 on Ed for updates:
  • The autograder denominator has been lowered from 24 to 22.
  • The deadline for the optional prediction competition in Question 3.4 has been moved to Monday 12/9.
• The Portfolio Homework is due on Saturday, and slip days are not allowed!
  Take a look at the feedback on your checkpoint submission on Gradescope! We'll open the submission portals on Gradescope by tomorrow.
• The Final Exam is on Thursday, December 12th.
  • 25-35% of the questions will be about pre-midterm content; the rest will be about post-midterm content.
  • You can bring 2 double-sided handwritten notes sheets.
  • We have two review sessions next week, one on Monday from 6:30-8:30PM and one on Tuesday from 5-7PM.

Please give us feedback! 🙏

• We're looking for your feedback to help improve the course for future offerings and decide where it sits in the overall EECS/DS curriculum.

• If at least 85% of the class fills out both:

  • This internal End-of-Semester Survey, and
  • the Official Campus Evaluations,
    

  then we will add 1% of extra credit to everyone's overall grade.

• The deadline to fill out both is on Tuesday, December 10th at 11:59PM.

Agenda

• Today's focus is on clustering, an unsupervised learning method. We'll focus on $k$-means clustering, the most popular clustering technique, but discuss another clustering technique (agglomerative clustering) as well.

• In our final lecture on Thursday, we'll give many examples of other techniques in machine learning that are small extensions to what we've covered so far.

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

Clustering

---

The taxonomy of machine learning

• In Lectures 14-22, we focused on building models for regression.
  In regression, we predict a continuous target variable, $y$, using some features, $X$.

• In the past few lectures, we switched our focus to building models for classification.
  In classification, we predict a categorical target variable, $y$, using some features, $X$.

• Both regression and classification are supervised learning methods.
  In both regression and classification, our goal is to predict $y$ from $X$. The datasets we've used already had a $y$ variable.

• What might an unsupervised learning problem look like?

Example: TV show ratings 📺

• Suppose we have the ratings that several customers of a streaming service gave to two popular TV shows: Modern Family and Stranger Things.

util.show_ratings()

• The data naturally falls into three groups, or clusters, based on users with similar preferences.
  All we're given are the ratings each customer gave to the two shows; the customers aren't already part of any group.

• If we ran the streaming service and could "identify" the three clusters, it could help inform us on who to make recommendations to.
  For example, if someone in the bottom-right cluster likes How I Met Your Mother, we might recommend it to other members of the bottom-right cluster since they have similar tastes.

• How do we algorithmically determine these clusters, especially when there are too many dimensions to visualize?

Clustering

• Goal: Given a set of $n$ data points stored as vectors in $\mathbb{R}^d$, $\vec x_1, \vec x_2, ..., \vec x_n$, and a positive integer $k$, place the data points into $k$ clusters of nearby points.
  In the scatter plot below, $n = 9$ and $d = 2$.

util.show_ratings()

• Think of clusters as colors; in other words, the goal of clustering is to assign each point a color, such that points of the same color are similar to one another.

• Note, unlike with regression or classification, there is no "right answer" that we're trying to predict – there is no $y$! This is what makes clustering unsupervised.

Centroids

• Idea: Points in a cluster should be close to the center of the cluster.
  The clustering method we're developing relies on this assumption.

• One technique for defining clusters involves choosing $k$ cluster centers, known as centroids.

  $$\vec \mu_1, \vec \mu_2, ..., \vec \mu_k \in \mathbb{R}^d$$

  For instance, $\vec \mu_2$ is the center of cluster 2.
  Cluster 2 might be the set of points colored blue, for instance.

• These $k$ centroids define the $k$ clusters; each data point "belongs" to the nearest centroid to it.

• Our problem reduces to finding the best locations for the centroids.
  Over the next few slides, we'll visualize several possible sets of centroids and the clusters they define.

• With the following $k = 3$ centroids, the data are colored in the way that we'd expect.

util.visualize_centroids([(2, 7), (8, 4), (8, 8)])

• But here, even though $k = 3$, the data are not colored "naturally"!

util.visualize_centroids([(2, 7), (8, 4), (3, 7)])

• Nothing is stopping us from setting $k = 2$, for instance!

util.visualize_centroids([(2, 7), (8, 4)])

• Or $k = 5$!

util.visualize_centroids([(4, 4), (5, 5), (6, 6), (7, 7), (8, 8)])

Reflections on choosing a centroid

• Some values of $k$ seemed more intuitive than others; $k$ is a hyperparameter that we'll need to tune.
  More on this later.

• For a fixed $k$, some clusterings "looked" better than others; we'll need a way to quantify this.

• As we did at the start of the second half of the course, we'll formulate an objective function to minimize. Specifically, we'll minimize inertia, $I$:

$$I(\vec \mu_1, \vec \mu_2, ..., \vec \mu_k) = \text{total squared distance} \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{of each point } \vec x_i \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{ to its closest centroid } \vec \mu_j$$

• Lower values of inertia lead to better clusterings; our goal is to find the set of centroids $\vec \mu_1, \vec \mu_2, ... \vec \mu_k$ that minimize inertia, $I$.

Activity

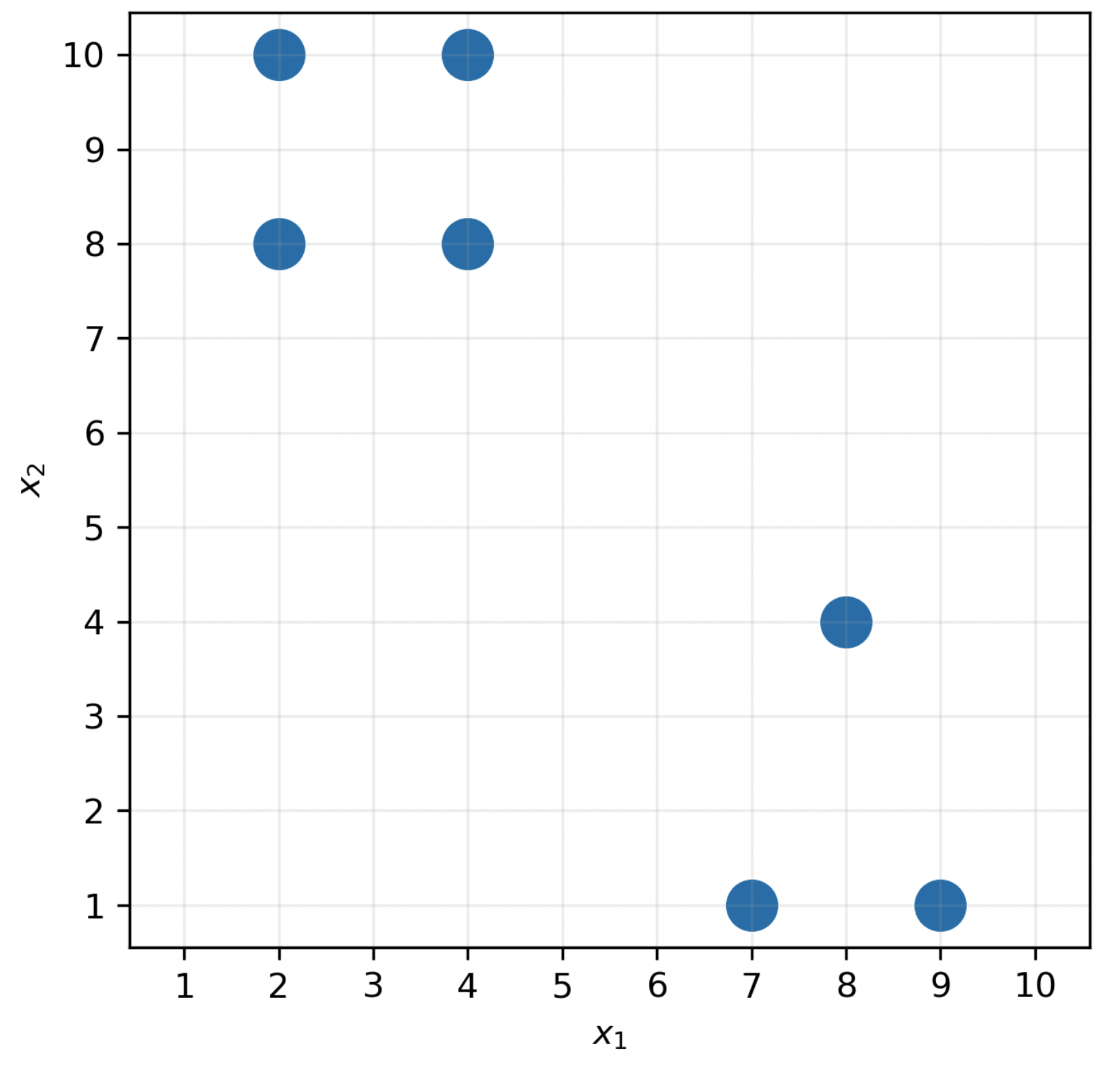
Recall, inertia is defined as follows:

$$I(\vec \mu_1, \vec \mu_2, ..., \vec \mu_k) = \text{total squared distance} \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{of each point } \vec x_i \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{ to its closest centroid } \vec \mu_j$$

Suppose we arrange the dataset below into $k = 2$ clusters. What is the minimum possible inertia?

$k$-means clustering

---

Minimizing inertia

• Goal: Find the centroids $\vec \mu_1, \vec \mu_2, ..., \vec \mu_k$ that minimize inertia:

$$I(\vec \mu_1, \vec \mu_2, ..., \vec \mu_k) = \text{total squared distance} \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{of each point } \vec x_i \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{ to its closest centroid } \vec \mu_j$$

• Issue: There is no efficient way to find the centroids that minimize inertia!

• There are $k^n$ possible assignments of points to clusters; it would be computationally infeasible to try them all.
  It can be shown that finding the optimal centroid locations is NP-hard.

• We can't use calculus to minimize $I$, either – we use calculus to minimize continuous functions, but the assignment of a point $\vec x_i$ to a centroid $\vec \mu_j$ is a discrete operation.

$k$-means clustering (i.e. Lloyd's algorithm)

• Fortunately, there's an efficient algorithm that (tries to) find the centroid locations that minimize inertia. The resulting clustering technique is called $k$-means clustering.
  Note that this has no relation to $k$-nearest neighbors, which we used for both regression and classification. Remember that clustering is an unsupervised technique!

1. Randomly initialize $k$ centroids.

2. Assign each point to the nearest centroid.

3. Move each centroid to the center of its group.

4. Repeat steps 2 and 3 until the centroids stop changing!
   This is an iterative algorithm!

• Let's visualize a few iterations ourselves.

util.visualize_centroids([(2, 5), (8, 10)], show_color=False, title='Step 1: Random Initialization<br>Red:(2, 5), Blue: (8, 10)')

util.visualize_centroids([(2, 5), (8, 10)], title='Iteration 1, Step 2: Assign each point to the nearest centroid<br>Red:(2, 5), Blue: (8, 10)')

util.visualize_centroids([(2, 5), (8, 10)], lines=True, title='Iteration 1, Step 2: Assign each point to the nearest centroid<br>Red:(2, 5), Blue: (8, 10); <b>Inertia = Sum(squared distances) = 156.25</b>')

util.visualize_centroids([(3.6, 6.8), (9.5, 7.125)], lines=True, assignments=[0] * 5 + [1] * 4, title='Iteration 1, Step 3: Move each centroid to the center of its group<br>Red:(3.6, 6.8), Blue: (9.5, 7.125); <b>Inertia = 85.1875</b>')

util.visualize_centroids([(3.6, 6.8), (9.5, 7.125)], assignments=[0] * 5 + [1] * 4, title='Iteration 1, Step 3: Move each centroid to the center of its group<br>Red:(3.6, 6.8), Blue: (9.5, 7.125); <b>Inertia = 85.1875</b>')

util.visualize_centroids([(3.6, 6.8), (9.5, 7.125)], title='Iteration 2, Step 2: Assign each point to the nearest centroid<br>Red:(3.6, 6.8), Blue: (9.5, 7.125); <b>Inertia = 70.653125</b>')

util.visualize_centroids([(2.5, 7.75), (9.2, 6.3)], title='Iteration 2, Step 3: Move each centroid to the center of its group<br>Red:(2.5, 7.75), Blue: (9.2, 6.3); <b>Inertia = 58.35</b>')

util.visualize_centroids([(2.5, 7.75), (9.2, 6.3)], title='Iteration 3, Step 2: Assign each point to the nearest centroid<br>No change, so algorithm terminates!')

Why does $k$-means work?

• On each iteration, inertia can only stay the same or decrease – it cannot increase.

$$I(\vec \mu_1, \vec \mu_2, ..., \vec \mu_k) = \text{total squared distance} \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{of each point } \vec x_i \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{ to its closest centroid } \vec \mu_j$$

• Why? Step 2 and step 3 alternate minimizing inertia in different ways:
  • In Step 2, we assign each point to the nearest centroid; this reduces the squared distance of each point to its closest centroid.
  • In Step 3, we move the centroids to the "middle" of their groups; this reduces the total squared distance from a centroid to the points assigned to it.

• Since there are only finitely many possible assignments of points to clusters, eventually the algorithm will terminate at some potentially local minimum.
  Read more on the theory here.

Let's experiment!

• Let's visualize more runs of the algorithm here.

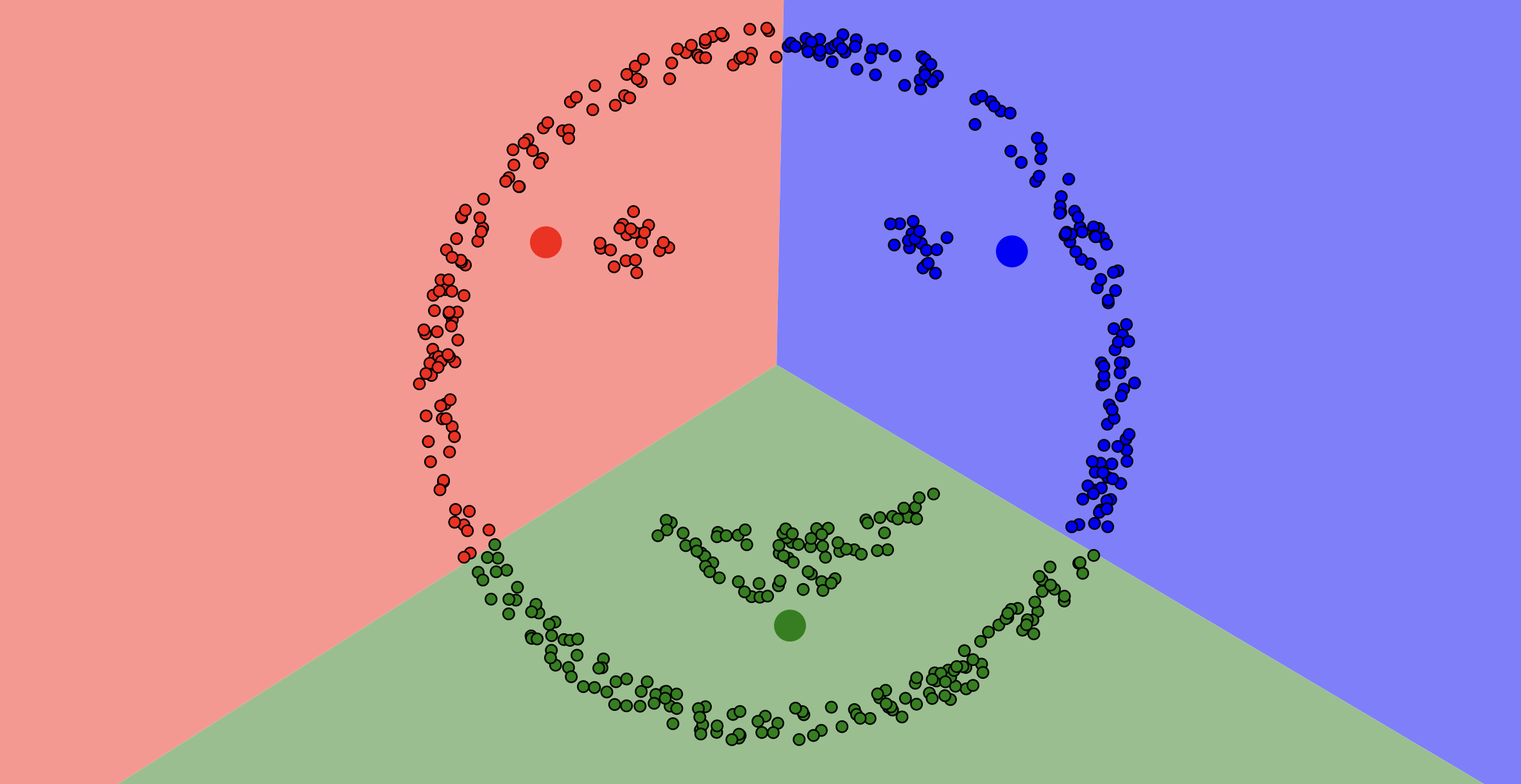
• To replicate the picture above, select "I'll Choose" and "Smiley Face."

In what sense is $k$-means optimal?

• The algorithm discussed isn't guaranteed to find the centroids that minimize inertia; depending on the initially-chosen centroids, it may converge at a local minimum.
  One solution is $k$-means++, which picks one centroid randomly and chooses the others in a way that maximizes distance from existing centroids. Read more here.

• Even if $k$-means "works", the resulting clustering might not look "right" to humans. That is, the clustering that minimizes inertia doesn't necessarily look correct to us.
  Remember, the core assumption in $k$-means is that points in a cluster should be close to the center of the cluster. This assumption isn't always true!

Choosing the number of clusters

---

Choosing $k$ in $k$-means clustering

• Given a dataset, how do we choose $k$, the number of clusters to use?

• The larger the value of $k$, the smaller inertia is.

$$I(\vec \mu_1, \vec \mu_2, ..., \vec \mu_k) = \text{total squared distance} \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{of each point } \vec x_i \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{ to its closest centroid } \vec \mu_j$$

• If $k = n$, then each point is a centroid, and inertia is 0!

• But, the goal of clustering is to put the data into groups, so a large number of groups may not be meaningful.

util.show_ratings()

The elbow method

• For several different values of $k$, let's compute the inertia of the resulting clustering, using the scatter plot from the previous slide.

util.show_elbow()

• The elbow method says to choose the $k$ that appears at the elbow of the plot of inertia vs. $k$, since there are diminishing returns for using more than $k$ clusters.
  Above, we see an elbow at $k = 3$, which gives us the $k$ that matches our natural intuition in this example.

• In practice, the data may not have natural clusters, so the choice of $k$ may not be so obvious.
  And, there may be other business reasons to choose a specific value of $k$, e.g. if you're told to categorize customers of a clothing item into 5 groups: XS, small, medium, large, XL.

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!

Example: World Bank data 🌎

---

Loading the data

• Below, we load in a dataset containing hundreds of attributes per country, taken from the World Bank.

world_bank = pd.read_csv('data/world_bank_data.csv').set_index('country').fillna(0)
world_bank

	Age dependency ratio (% of working-age population)	Age dependency ratio, old (% of working-age population)	Age dependency ratio, young (% of working-age population)	Bird species, threatened	...	Vulnerable employment, total (% of total employment) (modeled ILO estimate)	Wage and salaried workers, female (% of female employment) (modeled ILO estimate)	Wage and salaried workers, male (% of male employment) (modeled ILO estimate)	Wage and salaried workers, total (% of total employment) (modeled ILO estimate)
country
Algeria	57.51	10.02	47.49	15.0	...	26.76	73.73	68.16	69.06
Afghanistan	84.08	4.76	79.32	16.0	...	89.38	4.28	13.29	10.11
Albania	45.81	20.04	25.77	8.0	...	54.85	44.32	41.54	42.72
...	...	...	...	...	...	...	...	...	...
Yemen, Rep.	73.89	5.00	68.88	16.0	...	45.40	31.59	48.57	47.41
Zambia	88.81	3.96	84.84	20.0	...	77.78	11.98	31.14	21.92
Zimbabwe	82.95	5.38	77.57	19.0	...	65.65	24.14	43.18	33.87

217 rows × 209 columns

• There are $d = 209$ features, far too many to visualize before clustering.

world_bank.columns

Index(['Age dependency ratio (% of working-age population)',
       'Age dependency ratio, old (% of working-age population)',
       'Age dependency ratio, young (% of working-age population)',
       'Bird species, threatened',
       'Business extent of disclosure index (0=less disclosure to 10=more disclosure)',
       'Contributing family workers, female (% of female employment) (modeled ILO estimate)',
       'Contributing family workers, male (% of male employment) (modeled ILO estimate)',
       'Contributing family workers, total (% of total employment) (modeled ILO estimate)',
       'Cost of business start-up procedures (% of GNI per capita)',
       'Cost of business start-up procedures, female (% of GNI per capita)',
       ...
       'Unemployment, youth total (% of total labor force ages 15-24) (modeled ILO estimate)',
       'Urban population', 'Urban population (% of total population)',
       'Urban population growth (annual %)',
       'Vulnerable employment, female (% of female employment) (modeled ILO estimate)',
       'Vulnerable employment, male (% of male employment) (modeled ILO estimate)',
       'Vulnerable employment, total (% of total employment) (modeled ILO estimate)',
       'Wage and salaried workers, female (% of female employment) (modeled ILO estimate)',
       'Wage and salaried workers, male (% of male employment) (modeled ILO estimate)',
       'Wage and salaried workers, total (% of total employment) (modeled ILO estimate)'],
      dtype='object', length=209)

• Dimensionality reduction is another form of unsupervised learning that would help us visualize the data; we'll explore it briefly next class.

The elbow method, revisited

• How many clusters should we use? We'll need to resort to the elbow method, since we can't visualize the data to see how many "natural" clusters there are.

util.show_elbow_world_bank(world_bank)

• The choice is a bit more ambiguous than before; here, we'll use $k = 6$.

Clustering in sklearn

• To create our clusters, we'll use KMeans in sklearn.

from sklearn.cluster import KMeans

• Like other models we've used in sklearn, we need to instantiate and fit a KMeans object. The difference is that the fit method only takes in a single X, not an X and y.
  $k$-means is an unsupervised method, so there is no y.

# The default value of k is 8; we should generally specify another value.
# We fix a random_state for reproducibility; remember the centroids are generally initialized randomly.    
model = KMeans(n_clusters=6, random_state=15)
model.fit(world_bank)

KMeans(n_clusters=6, random_state=15)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• A fit KMeans instance has a predict method. It outputs the cluster whose centroid the data point is closest to.

model.predict(world_bank.loc[['United States']])

array([4], dtype=int32)

# It seems that the US and Canada are assigned to different clusters!
model.predict(world_bank.loc[['Canada']])

array([5], dtype=int32)

Inspecting clusters

• We can view the countries assigned to each cluster.

countries_and_clusters = pd.Series(model.labels_, index=world_bank.index)
util.list_countries_by_cluster(countries_and_clusters)

Cluster 0: Algeria, Afghanistan, Albania, American Samoa, Andorra, Angola, Antigua and Barbuda, Armenia, Aruba, Austria, Azerbaijan, Bahamas, The, Bahrain, Bangladesh, Barbados, Belarus, Belgium, Belize, Benin, Bermuda, Bhutan, Bolivia, Bosnia and Herzegovina, Botswana, British Virgin Islands, Brunei Darussalam, Bulgaria, Burkina Faso, Burundi, Cabo Verde, Cambodia, Cameroon, Cayman Islands, Central African Republic, Chad, Channel Islands, Chile, Colombia, Comoros, Congo, Dem. Rep., Congo, Rep., Costa Rica, Cote d'Ivoire, Croatia, Cuba, Curacao, Cyprus, Czech Republic, Denmark, Djibouti, Dominica, Dominican Republic, Ecuador, El Salvador, Equatorial Guinea, Eritrea, Estonia, Eswatini, Ethiopia, Faroe Islands, Fiji, Finland, French Polynesia, Gabon, Gambia, The, Georgia, Ghana, Gibraltar, Greece, Greenland, Grenada, Guam, Guatemala, Guinea, Guinea-Bissau, Guyana, Haiti, Honduras, Hong Kong SAR, China, Hungary, Iceland, Iran, Islamic Rep., Iraq, Ireland, Isle of Man, Israel, Jamaica, Jordan, Kazakhstan, Kenya, Kiribati, Korea, Dem. People’s Rep., Kosovo, Kuwait, Kyrgyz Republic, Lao PDR, Latvia, Lebanon, Lesotho, Liberia, Libya, Liechtenstein, Lithuania, Luxembourg, Macao SAR, China, Madagascar, Malawi, Maldives, Mali, Malta, Marshall Islands, Mauritania, Mauritius, Micronesia, Fed. Sts., Moldova, Monaco, Mongolia, Montenegro, Morocco, Mozambique, Myanmar, Namibia, Nauru, Nepal, New Caledonia, New Zealand, Nicaragua, Niger, North Macedonia, Northern Mariana Islands, Norway, Oman, Palau, Panama, Papua New Guinea, Paraguay, Peru, Portugal, Puerto Rico, Qatar, Romania, Rwanda, Samoa, San Marino, Sao Tome and Principe, Senegal, Serbia, Seychelles, Sierra Leone, Singapore, Sint Maarten (Dutch part), Slovak Republic, Slovenia, Solomon Islands, Somalia, South Africa, South Sudan, Sri Lanka, St. Kitts and Nevis, St. Lucia, St. Martin (French part), St. Vincent and the Grenadines, Sudan, Suriname, Sweden, Syrian Arab Republic, Tajikistan, Tanzania, Timor-Leste, Togo, Tonga, Trinidad and Tobago, Tunisia, Turkmenistan, Turks and Caicos Islands, Tuvalu, Uganda, Ukraine, United Arab Emirates, Uruguay, Uzbekistan, Vanuatu, Venezuela, RB, Vietnam, Virgin Islands (U.S.), West Bank and Gaza, Yemen, Rep., Zambia, Zimbabwe

Cluster 1: China

Cluster 2: Germany, India, Japan

Cluster 3: Brazil, France, Indonesia, Italy, Russian Federation, United Kingdom

Cluster 4: United States

Cluster 5: Argentina, Australia, Canada, Egypt, Arab Rep., Korea, Rep., Malaysia, Mexico, Netherlands, Nigeria, Pakistan, Philippines, Poland, Saudi Arabia, Spain, Switzerland, Thailand, Turkey

• It seems that the vast majority of countries are assigned to the same cluster!

Visualizing clusters

util.country_choropleth(countries_and_clusters)

Standardize before clustering!

• Clustering, like $k$-nearest neighbors and regularization, is a distance-based method, meaning that it depends on the scale of the data.

• In world_bank, some features are in the millions or billions, while some are in the single digits. The larger features will influence cluster membership more than the smaller features.

world_bank.iloc[[1], -9:-5]

	Urban population	Urban population (% of total population)	Urban population growth (annual %)	Vulnerable employment, female (% of female employment) (modeled ILO estimate)
country
Afghanistan	9.48e+06	25.5	3.35	95.57

• Solution: Standardize before clustering.

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline

model_std = make_pipeline(StandardScaler(), KMeans(n_clusters=6, random_state=15)) # We fix a random state for reproducibility.
model_std.fit(world_bank)

Pipeline(steps=[('standardscaler', StandardScaler()),
                ('kmeans', KMeans(n_clusters=6, random_state=15))])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

• Once we standarize, the sizes of the clusters seem to be a bit more evenly distributed!

countries_and_clusters_std = pd.Series(model_std[-1].labels_, index=world_bank.index)
util.list_countries_by_cluster(countries_and_clusters_std)

Cluster 0: Algeria, Albania, Antigua and Barbuda, Argentina, Armenia, Azerbaijan, Bahamas, The, Bahrain, Belize, Bolivia, Botswana, Brazil, Brunei Darussalam, Cabo Verde, Chile, Colombia, Costa Rica, Dominican Republic, Ecuador, Egypt, Arab Rep., El Salvador, Eswatini, Fiji, French Polynesia, Gabon, Georgia, Grenada, Guam, Guatemala, Guyana, Honduras, Indonesia, Iran, Islamic Rep., Iraq, Jamaica, Jordan, Kazakhstan, Kiribati, Korea, Dem. People’s Rep., Kuwait, Kyrgyz Republic, Lebanon, Libya, Malaysia, Maldives, Mauritius, Mexico, Micronesia, Fed. Sts., Moldova, Mongolia, Morocco, Namibia, New Caledonia, Nicaragua, Oman, Panama, Paraguay, Peru, Philippines, Qatar, Samoa, Sao Tome and Principe, Saudi Arabia, Seychelles, South Africa, Sri Lanka, St. Lucia, St. Vincent and the Grenadines, Suriname, Syrian Arab Republic, Tajikistan, Thailand, Tonga, Trinidad and Tobago, Tunisia, Turkey, Turkmenistan, United Arab Emirates, Uzbekistan, Vietnam, West Bank and Gaza

Cluster 1: American Samoa, Andorra, Aruba, Bermuda, British Virgin Islands, Cayman Islands, Curacao, Dominica, Faroe Islands, Gibraltar, Greenland, Isle of Man, Kosovo, Liechtenstein, Marshall Islands, Monaco, Nauru, Northern Mariana Islands, Palau, San Marino, Sint Maarten (Dutch part), St. Kitts and Nevis, St. Martin (French part), Turks and Caicos Islands, Tuvalu

Cluster 2: Afghanistan, Angola, Bangladesh, Benin, Bhutan, Burkina Faso, Burundi, Cambodia, Cameroon, Central African Republic, Chad, Comoros, Congo, Dem. Rep., Congo, Rep., Cote d'Ivoire, Djibouti, Equatorial Guinea, Eritrea, Ethiopia, Gambia, The, Ghana, Guinea, Guinea-Bissau, Haiti, Kenya, Lao PDR, Lesotho, Liberia, Madagascar, Malawi, Mali, Mauritania, Mozambique, Myanmar, Nepal, Niger, Nigeria, Pakistan, Papua New Guinea, Rwanda, Senegal, Sierra Leone, Solomon Islands, Somalia, South Sudan, Sudan, Tanzania, Timor-Leste, Togo, Uganda, Vanuatu, Venezuela, RB, Yemen, Rep., Zambia, Zimbabwe

Cluster 3: Australia, Austria, Barbados, Belarus, Belgium, Bosnia and Herzegovina, Bulgaria, Canada, Channel Islands, Croatia, Cuba, Cyprus, Czech Republic, Denmark, Estonia, Finland, France, Germany, Greece, Hong Kong SAR, China, Hungary, Iceland, Ireland, Israel, Italy, Japan, Korea, Rep., Latvia, Lithuania, Luxembourg, Macao SAR, China, Malta, Montenegro, Netherlands, New Zealand, North Macedonia, Norway, Poland, Portugal, Puerto Rico, Romania, Russian Federation, Serbia, Singapore, Slovak Republic, Slovenia, Spain, Sweden, Switzerland, Ukraine, United Kingdom, Uruguay, Virgin Islands (U.S.)

Cluster 4: United States

Cluster 5: China, India

Visualizing clusters after standardizing

• Note that the colors themselves are arbitrary.

util.country_choropleth(countries_and_clusters_std)

Agglomerative clustering

---

Overview of clustering methods

• sklearn supports many different clustering methods! Read about them all here.

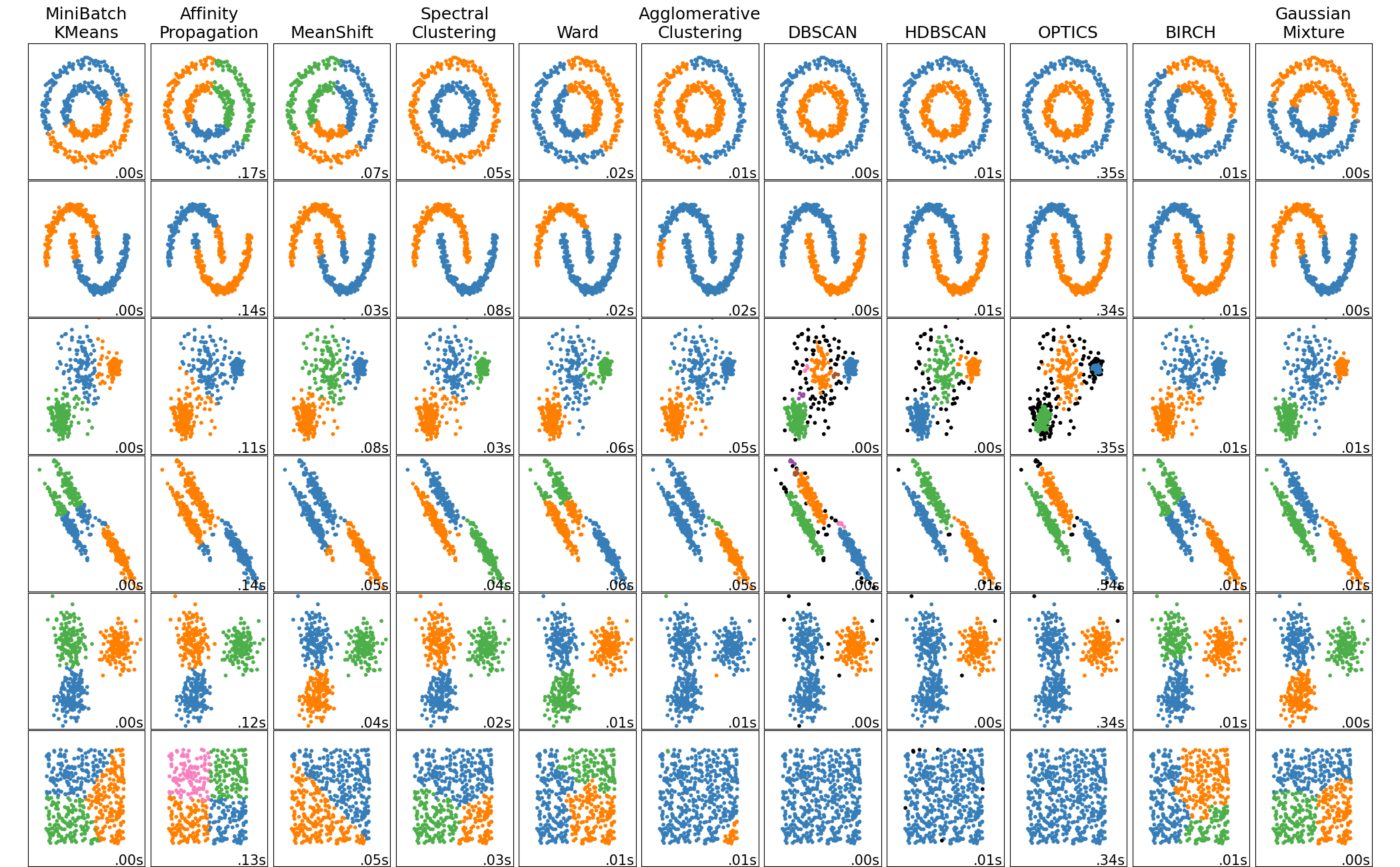
• Remember the "no free lunch theorem" – there isn't a clustering method that is always better than all other clustering methods. It depends on the data!

Agglomerative clustering

• Let's revisit the ratings dataset from earlier.

util.show_ratings()

• Agglomerative clustering, a form of hierarchical clustering, creates clusters by:
  1. Starting with each point as its own cluster.
  2. Repeatedly combining the two closest clusters until there are only $k$ clusters remaining.

• Let's visualize it in the context of this dataset!

util.color_ratings(title='Iteration 0')

• The two closest clusters are cluster 7 and cluster 8, so we merge them.

util.color_ratings(title='Iteration 1', labels=[0, 1, 2, 3, 4, 5, 6, 7, 7])

• Now, the two closest clusters are cluster 5 and cluster 6, so we merge them.

util.color_ratings(title='Iteration 2', labels=[0, 1, 2, 3, 4, 5, 5, 7, 7])

• It's not clear what the next merge should be – should cluster 4 merge with cluster 5 or should cluster 2 merge with cluster 3?

Linkage criteria

• We need a way to measure the distance between two clusters.
  For example, what is the "distance" between cluster 4 and cluster 5 below?

util.color_ratings(title='Iteration 2', labels=[0, 1, 2, 3, 4, 5, 5, 7, 7], width=500, height=400)

• The linkage criteria determines how to compute the distance between two clusters.

• Some examples:
  • Average linkage: The average distance between points in both clusters.
  • Single linkage: The minimum distance between points in both clusters.
  • Complete linkage: The maximum distance between points in both clusters.

util.color_ratings(title='Iteration 2', show_distances=[(1, 3), (0, 2), (0, 1), (2, 3), (4, 5)], labels=[0, 1, 2, 3, 4, 5, 5, 7, 7])

• We'll use single linkage, i.e.:

$$\text{distance(cluster $A$, cluster $B$)} = \text{minimum distance between} \\ \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \text{any point in $A$ and any point in $B$}$$

• Here, there are lots of ties; we'll arbitrarily choose to merge cluster 4 and cluster 5.

util.color_ratings(title='Iteration 3', show_distances=[(0, 2), (2, 3)], labels=[0, 1, 2, 3, 5, 5, 5, 7, 7])

• Again, there's a tie; we'll arbitrarily choose to merge cluster 2 and cluster 3.
  We could have also merged cluster 2 and cluster 0, since their minimum distance is also the same.

util.color_ratings(title='Iteration 4', show_distances=[(0, 2), (1, 2)], labels=[0, 1, 2, 2, 5, 5, 5, 7, 7])

• Next, we merge cluster 2 and cluster 0.
  Why? Because the minimum distance between cluster 0 and cluster 2 is less than the minimum distance between cluster 1 and cluster 2.

util.color_ratings(title='Iteration 5', labels=[2, 1, 2, 2, 5, 5, 5, 7, 7])

• And finally, we merge cluster 2 and cluster 1.

• If we just want $k = 3$ clusters, we stop here! If we wanted $k = 2$ clusters, we'd then merge the two closest clusters, based on the single linkage criterion.

$k$-means vs. agglomerative clustering

• On what sorts of datasets does agglomerative clustering perform better than $k$-means clustering?

util.show_scatter_comp()

util.show_scatter_comp_k_means(k=2)

• Note that $k$-means clustering optimizes for inertia, not "blobiness." It doesn't work well when the natural clusters are of uneven sizes.
  Read more here!

util.show_scatter_comp_agg(k=2)

• Another metric that's used to compare different clusterings is the silhouette score.
  Read more here!

Question 🤔 (Answer at practicaldsc.org/q)

Remember that you can always ask questions anonymously at the link above!